和積の公式の覚え方

　教科書などで和積の公式を見たことがある人は、「こんな公式を覚えるのか」と絶望的になったことでしょう。しかし実際には覚える必要がないどころか、その場で公式を作る必要もないのです。ただひとつ、変形のための方法を覚えるだけで良いのです。次の問題を考えてみましょう。

問． cos80°＋ cos40°を簡単にせよ

　突拍子も無い変形ですが、

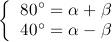とおいて、加法定理で展開すると

cos80°＋ cos40°

= cos(α+β) + cos(α-β)
= (cosαcosβ - sinαsinβ) + (cosαcosβ + sinαsinβ)
= 2cosαcosβ

となります。ところで α と β は

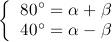を解けば、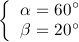

とわかるので、結局

cos80°＋ cos40°

= 2cosαcosβ
= 2cos60°cos20°
= cos20°

←( cos60°= )

となりました。この問題のように手のつけようがなく見える問題でも、2つの角を、 α + β , α - β とおいて展開するだけで、打開できることがあります。

　この方法ですべての和積の公式が作れます。

sin A + sin B

= sin(α+β) + sin(α-β) ←
= (sinαcosβ + cosαsinβ) + (sinαcosβ - cosαsinβ)
= 2sinαcosβ
= 2sincos

　　(3行目から4行目は、を α と β で解いて、として代入した。)

sin A - sin B

= sin(α+β) - sin(α-β)
= (sinαcosβ + cosαsinβ) - (sinαcosβ - cosαsinβ)
= 2cosαsinβ
= 2cossin

cos A + cos B

= cos(α+β) + cos(α-β)
= (cosαcosβ - sinαsinβ) + (cosαcosβ + sinαsinβ)
= 2cosαcosβ
= 2coscos

cos A - cos B

= cos(α+β) - cos(α-β)
= (cosαcosβ - sinαsinβ) - (cosαcosβ + sinαsinβ)
= -2sinαsinβ
= -2sinsin

いずれも、2つの角を、 α + β , α - β とおいて展開するだけなのですから、公式自体を覚える必要は全くないのです。

　この変形は、3倍角の公式を避けるのにも役に立ちます。

問、cos3x + cosx = 0 を解け。ただし 0°≦ x ＜ 360°とする。

　誰もが、「ああ、3倍角か」と思うでしょうが、3倍角の公式を覚えていなければ大変です。そんなとき、3x を α + β , x を α - β とおいてみましょう。

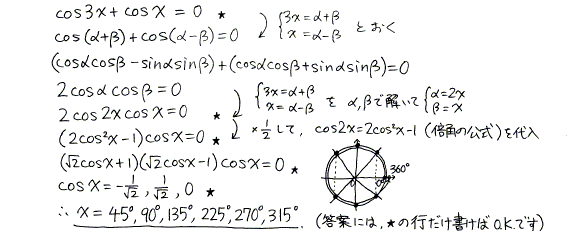
　また、上の計算によると、3倍角の公式を作ることもできます。

cos3x + cosx

= 2cos2x cosx
= 2(2cos²x - 1)cosx
= 4cos3x - 2cosx

　となりますから、cosx を移項して、 cos3x = 4cos³x - 3cosx とわかりますし、

sin3x + sinx

= 2sin2x cosx　　←変形は中略しました
= 2(2sinx cosx) cosx　　←倍角の公式　sin2x = 2sinx cosx
= 4sinx cos²x
= 4sinx (1 - sin²x )
= 4sinx - 4sin³x

として、sinx を移行すれば、 sin3x = 3sinx - 4sin³x となります。