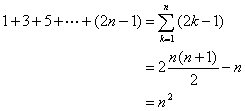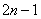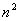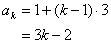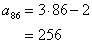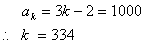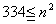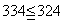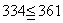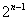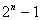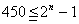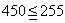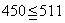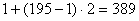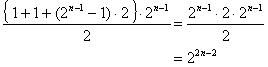令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
群数列の解法
群数列には大きく分けて二つのパターンがある。群の分け目をはずすと単純な数列になるものと,群の分け目をはずすと分かりにくくなるものだ。
(1)分け目をはずすと単純な数列になるもの例:{an}: 1|2,3|4,5,6|7,8,9,10|11,…
(2)分け目をはずすと分かりにくくなるもの
例:{an}: 1|1,2|1,2,3|1,2,3,4|1,…
ここではその両方に対応できる解法を説明する。
さて,群数列を解くときに必ず考えなければいけないことは3つある。
★ 第n群の中にいくつの項が入っているか
★ 第n群の終わりまでにいくつの項があるか
★ さらに(1)のパターンでは,分け目をはずしたときのkについての一般項akを,(2)のパターンでは第n群の中での一般項を考える。(1),(2)それぞれについて例題で説明する。
例題1群に分けられた数列
1|4,7,10|13,16,19,22,25|28,… がある。
(1) 第10群の第5項目を求めよ。
(2) 1000は第何群の第何項目か答えよ。
これは(1)のパターンであるが,最初に書いたとおり,まず考えるべきことは
第n群の中にいくつの項が入っているか
第n群の終わりまでにいくつの項があるか
である。まず第n群の中の項の数を考えよう。
1 4, 7, 10 13, 16, 19, 22, 25 群番号 1 2 3 … n 項数 1 3 5 … ?
こうしてみると,第n群の中の項数を並べたものは,初項1,公差2の等差数列になっているので,計算すれば
*
と言える。
次に第n群の終わりまでの項数だが,各群の中の項数を全部足せばよいから
(1行目の左辺に誤りがあり訂正しました。ご指摘下さった方、誠にありがとうございました。平成26年6月9日)
となる。これを先の表に埋めると次のようになる。
1 4, 7, 10 13, 16, 19, 22, 25 群番号 1 2 3 … n 項数 1 3 5 … 群末までの総項数
さて,これを頼りにして(1)を考えてみる。第10群の第5項目は,全体から見ると第何項目なのか? 「第9群までの項数+5」と考えればよい。第9群までの項数は81であるから,第10群の第5項目は全体から見れば第86項である。
第9群 第10群 …第81項 第82項…
全体から見た第86項はどんな数字か? それはこの数列の分け目をはずしたときの一般項を考えればすぐ分かる。この数列は群の分け目をはずせば,初項1,公差3の単純な等差数列で,その第k項は
となるから,第86項であれば
と計算できる。(一般項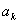 を求めずに,直接
を求めずに,直接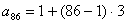 と計算しても良い。)
と計算しても良い。)
(2)ではまず,1000という数が,群の分け目をはずして全体から見たら第何項に当たるのかを求める。先に書いた一般項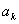 を用いて次のようにすればいい。
を用いて次のようにすればいい。
次に先の表を使って,全体から見た第334項が,第何群に入っているのかを調べる。もし第334項がn群までに入っているとすれば,それは334が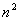 以下の数だということであるから,
以下の数だということであるから,
を計算すればいい。ここでおおざっぱに勘を働かせてnを考える。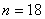 のときは
のときは
となって駄目だが,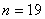 とすれば
とすれば
となるのでオーケーだ。これで1000という数字(この数列の第334項)は第19群に入っていることがわかった。
あとは第19群の中の何番目に出てくるかだが,それを知るためには第18群までに何項入っているのかを求めて,334からひいてやれば良い。すでに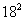 は計算してあってその値は324であった。すると334項は第19群の10番目とわかる。334から324をひいたわけである。
は計算してあってその値は324であった。すると334項は第19群の10番目とわかる。334から324をひいたわけである。
第18群 第19群 …第324項 第325項…
例題2群に分けられた数列
1 | 1, 3 | 1, 3, 5, 7 | 1, 3, 5, 7, 9, 11, 13, 15|1,3, ……がある。
(1) 第450項を求めよ
(2) 第n群の和をnで表わせ。
今度は「群の分け目を取り外すとわかりにくくなる数列」であるが,まず考えるべきことは前の例題と同様に
第n群の中にいくつの項が入っているか
第n群の終わりまでにいくつの項があるか
である。まず第n群の中の項の数を考えよう。
1 1, 3 1, 3, 5, 7 1, 3, 5, 7, 9, 11, 13, 15 … 群番号 1 2 3 4 … n 項数 1 2 4 8 … ?
こうしてみると,第n群の中の項数を並べたものは,初項1,公比2の等比数列になっているので,第n群の中の項数は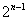 である。
である。
次に第n群の終わりまでの項数だが,各群の中の項数を全部足せばよいから
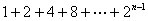
である。これは(ちょっと難しいが)初項1,公比2,項数nの等比数列の和なので,
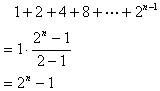
と計算できる。これらを先の表に埋めると次のようになる。
1 1, 3 1, 3, 5, 7 1, 3, 5, 7, 9, 11, 13, 15 … 群番号 1 2 3 4 … n 項数 1 2 4 8 … 群末までの総項数
あとはこの表の力を借りて問題を解くのである。
(1)は,この数列の第450項を求めさせようとしている。しかしこの数列は,群の分け目を取り外して一般項を求めようとしても無理である。群の分け目を取り外すと,
1 ,1, 3 ,1, 3, 5, 7 ,1, 3, 5, 7, 9, 11, 13, 15 ,1, 3,…
となって収拾がつかない。そこでまずは第450項が第何群に入っているかを探るのである。先の例題と同様に,第450項が第n群までに入っているとすると,次の式が成り立つ。
そこでこれを満たすnを勘で求める。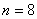 のとき,
のとき,
となり不適だが,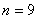 にすれば
にすれば
で適する。つまり第450項は第9群に入っているということだ。そして450から,第8群までの総項数をひけば,第9群の中の第何項目に位置するかが分かる。その計算は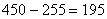 である。
である。
第8群 第9群 …第255項 第256項…
さて,あとは第9群の第195項が何であるかを答えるだけである。第9群は他の群と同じように,最初が1で,その後2ずつ増えていくはずでそれはつまり,初項1,公差2の等差数列ということだ。その初項1,公差2の等差数列の第195番目を答えろといわれているのだから,
である。
(2)では第n群内の総和を求めろといわれている。難しく思えるかもしれないが,良く考えてみると第n群とて実態は単なる「初項1,公差2」の等差数列だ。ただ,項数が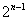 項である点だけがややこしい。それでも単に公式に代入することを考えれば次のように簡単に計算できる。
項である点だけがややこしい。それでも単に公式に代入することを考えれば次のように簡単に計算できる。
(第n群の中の末項が第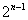 項なので
項なので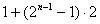 となるのである)
となるのである)