三角関数の合成

　三角関数の問題では、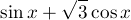sin x + square(3)cos xのような、sinx とcosx の一次式(?!)を、ひとつの三角関数にまとめなければならないことがよくあります。ここではまず、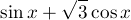sin x + square(3)cos xを、r sin(x + α)の形に変形することを考えましょう。

　r sin(x + α)は、加法定理で展開すると、

r sin(x + α) 　で、ちょっと並べ替えて
  　となります。これと
  　を見比べると、

　となればよいことが分かります。こうなるための r と α の求め方は、以前に説明したとおりで、

　つまり

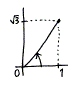　とわかるわけです。

このとき、

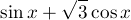sin x + square(3)cos x ですから、2でくくって並べ替えて、
  として、加法定理を逆向きに使うと、
  となります。

　一般に、 について、　となるような r と α を求めて、代入してやれば、

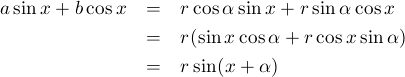
と、変形できるのです。要は、 を、加法定理を逆向きに使って無理矢理変形するために、　となる r と α を見つけるということです。


[御意見簡易送信窓]批判・激励・文句，なんでも歓迎。

2022年4月以降に動作ドラブル起きていることが判明しました。
現在復旧を試みています。ご連絡の方はツイッターなどをご利用ください。
その後にメッセージをお送り頂いた方には、深くお詫び申し上げます。(2022/11/3記す）

　メール(任意)
　名前(任意)

本文公開可 非公開希望 私信

確認欄←ここに""と入力してから、「OK」を押してください