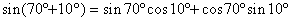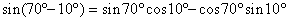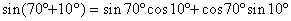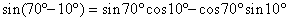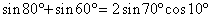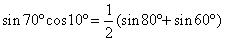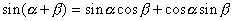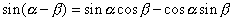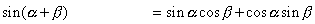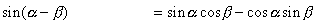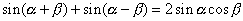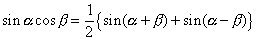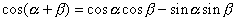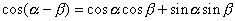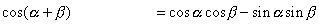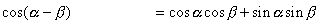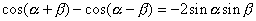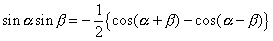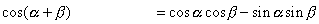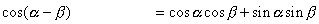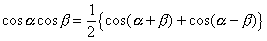令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
積和の公式の覚え方
問題 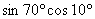 を和の形に直せ を和の形に直せ |
和積の公式は,二つの角を α + β , α - β とおいて加法定理で展開するだけの単純なものでしたが,積和の公式はどうでしょう.実は積和の公式も,公式をその場で作るというよりは,その計算方法を覚えておくものなのですが,和積の公式にくらべるとやや複雑です.とはいえ誰もが思っているほどには難しくはありません.
この問題の場合,まずはこの 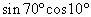 を含む加法定理の式を2つ書きます.
を含む加法定理の式を2つ書きます. 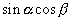 を含むのは,
を含むのは, 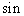 の加法定理で,
の加法定理で, 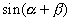 と
と 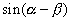 の2つだと気づかねばいけません.ここでは
の2つだと気づかねばいけません.ここでは 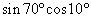 を含むものを書くので,
を含むものを書くので, 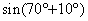 と
と 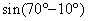 の2つで,それらの式は
の2つで,それらの式は
となります.さて,この2式から, 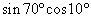 を残して
を残して 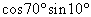 を消すにはどうしたらよいでしょう? それには両辺をたすことになります.ついでに左辺の
を消すにはどうしたらよいでしょう? それには両辺をたすことになります.ついでに左辺の 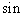 について,
について, 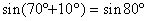 ,
, 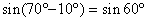 と計算してしまいましょう.すると,
と計算してしまいましょう.すると,
+) (←括弧の中は普通に計算した)
となりますから,左右を入れ替えて両辺を 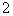 でわれば,
でわれば,
となり,変形が終わりました.あとは 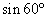 を
を 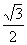 になおしてカッコを展開すれば完璧です.
になおしてカッコを展開すれば完璧です.
このように,与えられた積を含む加法定理の式2つを,たすかひくことが,積から和の形に直すときのポイントです.
この方法で全ての積和の公式が作れます.
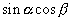 |
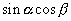 が登場する加法定理の式は,先に言ったように
が登場する加法定理の式は,先に言ったように 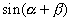 と
と 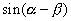 の2つですから,まずこれらを並べて書きます.すると
の2つですから,まずこれらを並べて書きます.すると
となり, 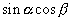 を残すには2式をたせばいいので,
を残すには2式をたせばいいので,
+)
となり,左右を入れ替えて両辺を 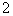 でわると
でわると
という公式ができました.
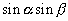 |
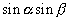 が登場する加法定理の式は,
が登場する加法定理の式は, 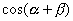 と
と 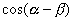 の2つです.
の2つです.
ここで 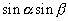 を残すためには
を残すためには 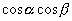 を消すことになるので,2式を引き算せねばなりません.
を消すことになるので,2式を引き算せねばなりません.
−)
この場合は左右を入れ替えて両辺を 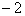 でわって,
でわって,
です.
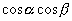 |
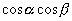 が登場するのも
が登場するのも 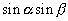 と同様,
と同様, 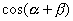 と
と 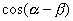 の2つです.
の2つです. 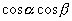 を残すためには,両辺をたすことになります.
を残すためには,両辺をたすことになります.
+)
これを左右入れ替えて両辺を 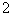 でわれば
でわれば
というわけです.
ここでは一応公式を書いておきましたが,先に述べたようにに公式を丸暗記するのではなく,与えられた積を含む加法定理の式2つを,たすかひくと覚えておけばよいわけです.