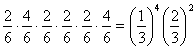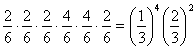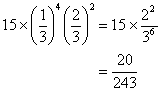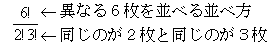反復試行の確率

問題　立方体の６面のうち，１つの面を赤で，２つの面を黄で，３つの面を青でぬる。

(1)　この立方体を6回投げたとき，黄が4回出る確率を求めよ。

(2)　この立方体を6回投げたとき，赤が１回，黄が2回，青が3回出る確率を求めよ。

同じことをくり返し行って，そのうち何回Ａが起きて，Ｂが起きて……という確率を反復試行の確率という。

反復試行の場合，その起こり方が何通りあるかをまず考えねばならない。例えば問題(1)の場合

　　　　　

と出てもいいし，または

　　　　　

と出てもいい。(注：問題(1)で，赤と青についてはどちらが出ても，黄色の出る回数には関係がないので，まとめて考えている。)他にもいっぱいあるのでいちいち数えるわけには行かないので，個数の処理で行くことにする。

　　　　……４枚

　　　　……２枚　計６枚

を並べる並べ方を考えればいいので

となる。つまり15通りの｢または｣があるわけである。

次に，出かた一通り当たりの確率を考える。

例えば　　　　　の順番で出る確率は，

であるし，　　　　　の順番で出る確率は

であるし，他の出かたでも同じように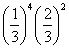になる。(確率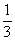の事象が４回と，確率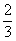の事象が２回，と考えれば良い)。要するに，さっき計算した15通りのそれぞれの出かたについて確率が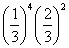なので，これを15回たす，つまり15をかけてやれば，

となる。つまり

　反復試行の確率＝出かたの通り数×一通り当たりの確率

と計算したわけである。

問題(2)も基本的に同じである。出かたについては　　　　　の順で出ても，　　　　　の順で出てもいいわけで，その出かたは

　……１枚

　……２枚

　……３枚　　計６枚

を並べる並べ方を考えて，

である。そしてその一通り当たりの確率が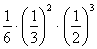なので，求める確率は

となる。

反復試行の確率＝出かたの通り数(カードの並べ方の順列)× 一通り当たりの確率

練習問題

袋の中に大当たりくじが１本と，小当たりくじが２本と，はずれくじが５本入っている。このくじを１本ずつひいてはもとに戻し，計６回ひくとき，

(1) はずれを３回だけひく確率をもとめよ。

(2) 大当たり・小当たり・はずれを各二回ずつひく確率を求めよ。