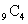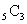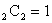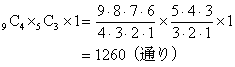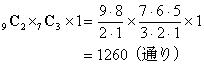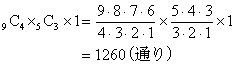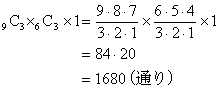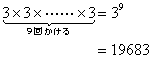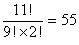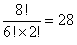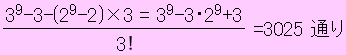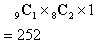д»Өе’Ң4е№ҙ3жңҲ11ж—Ҙ: жқұж—Ҙжң¬еӨ§йңҮзҒҪгғҲгғӘгӮўгғјгӮёиЁҙиЁҹгӮ’жҺІијү
зө„гҒҝеҲҶгҒ‘е…Ёгғ‘гӮҝгғјгғі
зөҗж§ӢеӨ§еӨүгҒ§гҒӮгӮӢгҒҢпјҢеҮәжқҘгӮҢгҒ°д»ҘдёӢгҒ®е°‘гҒӘгҒҸгҒЁгӮӮ(9)гҒҫгҒ§гӮ’гғһгӮ№гӮҝгғјгҒ—гҒҹгҒ„гӮӮгҒ®гҒ§гҒӮгӮӢгҖӮ
| е•ҸйЎҢгҖҖ9еҖӢгҒ®зҺүгӮ’3зө„гҒ«еҲҶгҒ‘гӮӢгҒ“гҒЁгӮ’иҖғгҒҲгӮӢгҖӮ (1)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢAгҒ•гӮ“гҒ«4еҖӢпјҢBгҒ•гӮ“гҒ«3еҖӢпјҢCгҒ•гӮ“гҒ«2еҖӢеҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ (2)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ4еҖӢпҪҘ3еҖӢпҪҘ2еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ (3)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢAгҒ•гӮ“гҒ«3еҖӢпјҢBгҒ•гӮ“гҒ«3еҖӢпјҢCгҒ•гӮ“гҒ«3еҖӢеҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ (4)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ3еҖӢпҪҘ3еҖӢпҪҘ3еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ (5)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ1еҖӢпҪҘ4еҖӢпҪҘ4еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ (6)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгӮҲгҒ„гҖӮ (7)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҜгҒ„гҒӘгҒ„гӮӮгҒ®гҒЁгҒҷгӮӢгҖӮ (8)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’пјҢ3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгӮҲгҒ„гҖӮ (9)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’пјҢ3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҜгҒ„гҒӘгҒ„гӮӮгҒ®гҒЁгҒҷгӮӢгҖӮ (10)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—зө„гҒ«еҢәеҲҘгҒҜд»ҳгҒ‘гҒҡпјҢ0еҖӢгҒ®зө„гҒҜгҒӮгҒЈгҒҰгҒҜгҒӘгӮүгҒӘгҒ„гҖӮ (11)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—зө„гҒ«еҢәеҲҘгҒҜд»ҳгҒ‘гҒҡпјҢ0еҖӢгҒ®зө„гҒҜгҒӮгҒЈгҒҰгҒҜгҒӘгӮүгҒӘгҒ„гҖӮ |
вҳ…е№іжҲҗ29е№ҙ11жңҲ9ж—ҘиҝҪеҠ пјҡ(11)гҒ®е•ҸйЎҢгҒ«еҜҫгҒ—пјҢиӘӯиҖ…гҒ®ж–№гҒӢгӮүд»ҘеүҚгҒ“гҒЎгӮүгҒ§зҙ№д»ӢгҒ—гҒҰгҒ„гҒҹи§Јжі•гӮҲгӮҠгӮӮзҫҺгҒ—гҒ„иҖғгҒҲж–№гӮ’ж•ҷгҒҲгҒҰй ӮгҒҚгҒҫгҒ—гҒҹгҖӮеҪ“йқўгҒ“гҒ®иҝҪиЁҳ(гҒ“гҒ®ж–Ү)гҒЁпјҢ(11)гҒ®зҫҺгҒ—гҒ„и§Јжі•гӮ’иҝҪеҠ гҒ—гҒҹзҠ¶ж…ӢгҒ§гҒҠгҒ„гҒҰгҒҠгҒҚгҒҫгҒҷгҖӮ
гҖҖзө„гҒҝеҲҶгҒ‘гҒ®е•ҸйЎҢгҒ«гҒҜпјҢгҒ„гӮҚгҒ„гӮҚгҒӘгғ‘гӮҝгғјгғігҒҢгҒӮгӮӢгҒҢпјҢгҒқгӮҢгӮүгӮ’гҒІгҒЁгҒҫгҒЁгӮҒгҒ«гҒ—гҒҰиӘ¬жҳҺгҒ•гӮҢгҒҹгҒ“гҒЁгҒҜгҒӘгҒ„гҒЁжҖқгҒҶгҖӮгҒқгҒ“гҒ§гҒ“гҒ“гҒ§гҒҜгҒқгӮҢгӮүгӮ’гҒҚгҒЎгӮ“гҒЁгғ‘гӮҝгғјгғіеҲҶгҒ‘гҒ—гҒҰгҒҠгҒ“гҒҶгҖӮгҒқгҒ—гҒҰзҗҶи§ЈгҒҷгӮӢгҒ№гҒҚгҒ“гҒЁгӮ’гҒҫгҒЁгӮҒгҒҹгҒ®гҒҢж¬ЎгҒ®иЎЁгҒ§гҒӮгӮӢгҖӮ
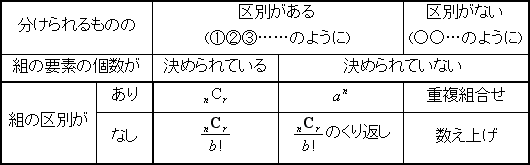
гҖҖaгҒҜзө„гҒ®ж•°пјҢbгҒҜеҢәеҲҘгҒ®гҒӨгҒҸзө„гҒ®ж•°гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒ“гӮҢгҒ§гҒҜдҪ•гҒ®гҒ“гҒЁгҒ гҒӢгӮҸгҒӢгӮүгҒӘгҒ„гҒ§гҒӮгӮҚгҒҶгҒӢгӮүпјҢдёҖгҒӨдёҖгҒӨи§ЈиӘ¬гҒ—гҒҰгҒ„гҒҸгҒ“гҒЁгҒ«гҒҷгӮӢгҖӮ
| (1)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’AгҒ•гӮ“гҒ«4еҖӢпјҢBгҒ•гӮ“гҒ«3еҖӢпјҢCгҒ•гӮ“гҒ«2еҖӢеҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ |
гҖҖгҒЁгӮҠгҒӮгҒҲгҒҡз•°гҒӘгӮӢ9еҖӢгҒӢгӮүпјҢAгҒ•гӮ“гҒ«жёЎгҒҷзҺүгӮ’4еҖӢйҒёгҒјгҒҶгҖӮ
гҖҖж¬ЎгҒ«ж®ӢгҒЈгҒҹ4еҖӢгҒӢгӮүпјҢBгҒ•гӮ“гҒ«жёЎгҒҷзҺүгӮ’3еҖӢйҒёгҒ¶гҖӮ
гҖҖжңҖеҫҢгҒ«ж®ӢгҒЈгҒҹ2еҖӢгҒӢгӮүпјҢCгҒ•гӮ“гҒ«жёЎгҒҷзҺүвҖҰвҖҰгҒ“гӮҢгҒҜгӮӮгҒҶйҒёгҒ¶дҪҷең°гҒҜгҒӘгҒҸпјҢ1йҖҡгӮҠгҒ§гҒӮгӮӢгҖӮ
гҖҖгҒ“гҒ®3гҒӨгҒ®дҪңжҘӯгҒҜйҖЈз¶ҡж“ҚдҪңгҒӘгҒ®гҒ§пјҢе…ЁйғЁжҺӣгҒ‘з®—гҒ—гҒҰ
гҒЁгҒҷгӮҢгҒ°OKгҒ§гҒӮгӮӢгҖӮ
(жіЁ:еҲҶгҒ‘гӮӢж•°гҒ®е°‘гҒӘгҒ„CгҒ•гӮ“гҒ®еҲҶгҒӢгӮүйҒёгҒ¶гҒ»гҒҶгҒҢпјҢиЁҲз®—ејҸгҒҜз°ЎеҚҳгҒ«гҒӘгӮӢгҖӮгҒқгҒ®е ҙеҗҲгҒ®иЁҲз®—гҒҜ
гҒЁгҒӘгӮӢгҖӮ)
гҖҖгҒ“гҒ®е•ҸйЎҢгҒ§гҒҜпјҢ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’3дәәгҒ«еҲҶгҒ‘гӮӢгҒЁгҒ„гҒҶгҒ“гҒЁгҒӘгҒ®гҒ§пјҢеҲҶгҒ‘гӮүгӮҢгӮӢгӮӮгҒ®(зҺү)гҒ«еҢәеҲҘгҒҢгҒӮгҒЈгҒҰпјҢзө„(дәәй–“)гҒ«гӮӮеҢәеҲҘгҒҢгҒӮгӮӢгҒЁгҒ„гҒҶгӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮгҒ—гҒӢгӮӮзө„еҶ…гҒ®иҰҒзҙ гҒ®еҖӢж•°гҒҢжұәгҒҫгҒЈгҒҰгҒ„гӮӢгҒ®гҒ§пјҢгҒқгҒ®зө„гҒ«жұәгӮҒгӮүгӮҢгҒҹеҖӢж•°гҒҡгҒӨйҒёгӮ“гҒ§гӮҶгҒҸгҒ гҒ‘гҒ§гӮҲгҒ„гҒ®гҒ§гҒӮгӮӢгҖӮ
| (2)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’4еҖӢпҪҘ3еҖӢпҪҘ2еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ |
гҖҖе®ҹгҒҜгҒ“гҒ®е ҙеҗҲгӮӮ(1)гҒЁгҒҫгҒЈгҒҹгҒҸеҗҢгҒҳгҒ§пјҢгҒҫгҒҡз•°гҒӘгӮӢ9еҖӢгҒӢгӮү4еҖӢгҒ®зө„гӮ’йҒёгӮ“гҒ§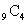 йҖҡгӮҠпјҢж¬ЎгҒ«ж®ӢгҒЈгҒҹ4еҖӢгҒӢгӮү3еҖӢгҒ®зө„гӮ’дҪңгҒЈгҒҰ
йҖҡгӮҠпјҢж¬ЎгҒ«ж®ӢгҒЈгҒҹ4еҖӢгҒӢгӮү3еҖӢгҒ®зө„гӮ’дҪңгҒЈгҒҰ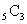 йҖҡгӮҠпјҢжңҖеҫҢгҒ«ж®ӢгҒЈгҒҹ2еҖӢгҒҢгҒқгҒ®гҒҫгҒҫ2еҖӢгҒ®зө„гҒ«гҒӘгӮӢгӮҸгҒ‘гҒӘгҒ®гҒ§пјҢ
йҖҡгӮҠпјҢжңҖеҫҢгҒ«ж®ӢгҒЈгҒҹ2еҖӢгҒҢгҒқгҒ®гҒҫгҒҫ2еҖӢгҒ®зө„гҒ«гҒӘгӮӢгӮҸгҒ‘гҒӘгҒ®гҒ§пјҢ
гҒ§гҒ„гҒ„гӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮгҒ“гҒ®е ҙеҗҲгӮӮпјҢ4еҖӢгҒ®зө„гғ»3еҖӢгҒ®зө„гғ»2еҖӢгҒ®зө„гҒҢе…ЁйғЁйҒ•гҒҶзө„(зҺүгҒ®еҖӢж•°гҒҢйҒ•гҒҶ)гҒӘгҒ®гҒ§пјҢдәәгҒ«жёЎгҒҷгҒ®гҒ§гҒҜгҒӘгҒ„гҒ‘гӮҢгҒ©гӮӮпјҢзө„гҒ®еҢәеҲҘгҒҢгҒӨгҒҸгҒЁгҒ„гҒҶзӮ№гҒ§(1)гҒЁеҗҢгҒҳгҒӘгҒ®гҒ§гҒӮгӮӢгҖӮ
| (3)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’AгҒ•гӮ“гҒ«3еҖӢпјҢBгҒ•гӮ“гҒ«3еҖӢпјҢCгҒ•гӮ“гҒ«3еҖӢеҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ |
гҖҖгҒ“гӮҢгӮӮж–№жі•гҒҜ(1)гӮ„(2)гҒЁгҒҫгҒЈгҒҹгҒҸеҗҢгҒҳгҒ§гҒӮгӮӢгҖӮAгҒ•гӮ“пјҢBгҒ•гӮ“пјҢCгҒ•гӮ“гҒҜдәәй–“гҒ§еҢәеҲҘгҒҢгҒӮгӮӢгҒ®гҒ§пјҢгҒҫгҒҡAгҒ•гӮ“гҒ«дёҺгҒҲгӮӢ3еҖӢгӮ’йҒёгӮ“гҒ§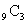 йҖҡгӮҠгҖӮж®ӢгҒЈгҒҹ6еҖӢгҒӢгӮүBгҒ•гӮ“гҒ®3еҖӢгӮ’йҒёгҒ№гҒ°
йҖҡгӮҠгҖӮж®ӢгҒЈгҒҹ6еҖӢгҒӢгӮүBгҒ•гӮ“гҒ®3еҖӢгӮ’йҒёгҒ№гҒ°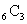 йҖҡгӮҠгҖӮжңҖеҫҢгҒ«ж®ӢгҒЈгҒҹ3еҖӢгҒҢCгҒ•гӮ“гҒ®гӮӮгҒ®гҒ«гҒӘгӮӢгҒӢгӮүпјҢ
йҖҡгӮҠгҖӮжңҖеҫҢгҒ«ж®ӢгҒЈгҒҹ3еҖӢгҒҢCгҒ•гӮ“гҒ®гӮӮгҒ®гҒ«гҒӘгӮӢгҒӢгӮүпјҢ
гҒ§гҒӮгӮӢгҖӮ
| (4)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ3еҖӢпҪҘ3еҖӢпҪҘ3еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ |
гҖҖгҒ“гҒ®е ҙеҗҲгҒҜ(1)гӮ„(2)гӮ„(3)гҒЁгҒҜгҒЎгӮҮгҒЈгҒЁйҒ•гҒҶгҒ®гҒ§гҒӮгӮӢгҖӮ3гҒӨгҒ®зө„гҒҜеҖӢж•°гҒҢеҗҢгҒҳгҒӘгҒ®гҒ§пјҢгҒқгӮҢгҒһгӮҢгҒ®зө„гҒ«йҒ•гҒ„гҒҢгҒӘгҒ„гҒ®гҒ§гҒӮгӮӢгҖӮзө„гҒ®еҢәеҲҘгҒҢгҒӨгҒӢгҒӘгҒ„гӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒ—гҒӢгҒ—гҒҜгҒҳгӮҒгҒӢгӮүзө„гҒ«еҢәеҲҘгҒҢгҒӘгҒ„гӮӮгҒ®гҒЁгҒ—гҒҰеҲҶгҒ‘гӮӢгҒ®гҒҜйӣЈгҒ—гҒ„гҒ®гҒ§пјҢеҗ„зө„гҒ«д»®гҒ®зңӢжқҝAпҪҘBпҪҘCгӮ’гҒӨгҒ‘гҒҰеҲҶгҒ‘гӮӢгҒ“гҒЁгӮ’иҖғгҒҲгӮӢгҖӮгҒқгҒҶгҒҷгӮҢгҒ°(3)гҒЁеҗҢгҒҳгҒӘгҒ®гҒ§
пјҲйҖҡгӮҠпјү
гҒЁиЁҲз®—гҒ§гҒҚгӮӢгҖӮгҒЁгҒ“гӮҚгҒҢе®ҹйҡӣгҒ«гҒҜзө„гҒ«еҢәеҲҘгҒҢгҒӘгҒ„гҒ®гҒ§пјҢ9еҖӢгҒ®зҺү гҖң
гҖң гҒҢпјҢдҫӢгҒҲгҒ°ж¬ЎгҒ®иЎЁгҒ®гӮҲгҒҶгҒ«еҲҘгӮҢгҒҰгҒ—гҒҫгҒЈгҒҹе ҙеҗҲгҒҜпјҢд»®гҒ«д»ҳгҒ‘гҒҰгҒҠгҒ„гҒҹзө„гҒ®зңӢжқҝABCгӮ’гҒҜгҒҡгҒ—гҒҰгҒ—гҒҫгҒҶгҒЁпјҢгҒҫгҒЈгҒҹгҒҸеҗҢгҒҳзө„гҒҝеҲҶгҒ‘гҒ«гҒӘгҒЈгҒҰгҒ—гҒҫгҒҶгҒ®гҒ§гҒӮгӮӢгҖӮ
гҒҢпјҢдҫӢгҒҲгҒ°ж¬ЎгҒ®иЎЁгҒ®гӮҲгҒҶгҒ«еҲҘгӮҢгҒҰгҒ—гҒҫгҒЈгҒҹе ҙеҗҲгҒҜпјҢд»®гҒ«д»ҳгҒ‘гҒҰгҒҠгҒ„гҒҹзө„гҒ®зңӢжқҝABCгӮ’гҒҜгҒҡгҒ—гҒҰгҒ—гҒҫгҒҶгҒЁпјҢгҒҫгҒЈгҒҹгҒҸеҗҢгҒҳзө„гҒҝеҲҶгҒ‘гҒ«гҒӘгҒЈгҒҰгҒ—гҒҫгҒҶгҒ®гҒ§гҒӮгӮӢгҖӮ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Aзө„ |    |
   |
   |
   |
   |
   |
| Bзө„ |    |
   |
   |
   |
   |
   |
| Cзө„ |    |
   |
   |
   |
   |
   |
гҖҖдёҠгҒ®иЎЁгҒ§гҒҜпјҢгҖҢAзө„гҖҚгҖҢBзө„гҖҚгҖҢCзө„гҖҚгҒЁгҒ„гҒҶзңӢжқҝгҒҢгҒӮгӮӢгҒӢгӮүгҒ“гҒқпјҢеҲҘгҖ…гҒ®еҲҶгҒ‘ж–№гҒ«иҰӢгҒҲгӮӢгҒҢпјҢзө„еҗҚгӮ’гҒҜгҒҡгҒ—гҒҹгӮү
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Г—зө„ |    |
   |
   |
   |
   |
   |
| Г—зө„ |    |
   |
   |
   |
   |
   |
| Г—зө„ |    |
   |
   |
   |
   |
   |
гҒ©гҒ®еҲҶгҒ‘ж–№гҒ§гӮӮгҖҢ

 гҒ®зө„гҖҚгҒЁгҖҢ
гҒ®зө„гҖҚгҒЁгҖҢ

 гҒ®зө„гҖҚгҒЁгҖҢ
гҒ®зө„гҖҚгҒЁгҖҢ

 гҒ®зө„гҖҚгҒҢгҒӮгӮӢгҒ гҒ‘гҒ§гҒӮгӮӢгҖӮ
гҒ®зө„гҖҚгҒҢгҒӮгӮӢгҒ гҒ‘гҒ§гҒӮгӮӢгҖӮ
гҖҖд»®гҒ®зңӢжқҝгӮ’д»ҳгҒ‘гҒҰгҒ„гҒҹгҒЁгҒҚгҒҜпјҢ

 гҒ®зө„гҒЁ
гҒ®зө„гҒЁ

 гҒ®зө„гҒЁ
гҒ®зө„гҒЁ

 гҒ®зө„гҒқгӮҢгҒһгӮҢгҒ«пјҢд»®гҒ®зңӢжқҝAпҪҘBпҪҘCгҒ®д»ҳгҒ‘ж–№гҒ®ж–№жі•гҒ®ж•°гҒ гҒ‘дҪҷиЁҲгҒ«ж•°гҒҲгҒҰгҒ„гҒҹгҒЁгҒ„гҒҶгӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮгҒқгҒ®зңӢжқҝгҒ®д»ҳгҒ‘ж–№гҒҜAпҪҘBпҪҘCгҒ®3ж–Үеӯ—гҒ®дёҰгҒ№ж–№гҒ®ж•°гҒ гҒ‘гҒӮгӮӢгҒҜгҒҡгҒӘгҒ®гҒ§пјҢ3!йҖҡгӮҠгҒӮгӮӢгҒ“гҒЁгҒ«гҒӘгӮӢгҖӮгҒӨгҒҫгӮҠпјҢ
гҒ®зө„гҒқгӮҢгҒһгӮҢгҒ«пјҢд»®гҒ®зңӢжқҝAпҪҘBпҪҘCгҒ®д»ҳгҒ‘ж–№гҒ®ж–№жі•гҒ®ж•°гҒ гҒ‘дҪҷиЁҲгҒ«ж•°гҒҲгҒҰгҒ„гҒҹгҒЁгҒ„гҒҶгӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮгҒқгҒ®зңӢжқҝгҒ®д»ҳгҒ‘ж–№гҒҜAпҪҘBпҪҘCгҒ®3ж–Үеӯ—гҒ®дёҰгҒ№ж–№гҒ®ж•°гҒ гҒ‘гҒӮгӮӢгҒҜгҒҡгҒӘгҒ®гҒ§пјҢ3!йҖҡгӮҠгҒӮгӮӢгҒ“гҒЁгҒ«гҒӘгӮӢгҖӮгҒӨгҒҫгӮҠпјҢ
| зө„гҒ®еҢәеҲҘгҒҢгҒӮгӮӢгҒЁгҒҚгҒ®3!йҖҡгӮҠгҖҖвҶ’гҖҖзө„гҒ®еҢәеҲҘгҒҢгҒӘгҒ„гҒЁгҒҚгҒ®1йҖҡгӮҠ |
гҒЁгҒ„гҒҶй–ўдҝӮгҒ§гҒӮгӮӢгҒ“гҒЁгҒҢеҲҶгҒӢгӮӢгҖӮгҒ“гӮҢгҒҜгҖҢ

 гҒ®зө„гҖҚгҒЁгҖҢ
гҒ®зө„гҖҚгҒЁгҖҢ

 гҒ®зө„гҖҚгҒЁгҖҢ
гҒ®зө„гҖҚгҒЁгҖҢ

 гҒ®зө„гҖҚгҒ®гӮҲгҒҶгҒӘпјҢгҒ»гҒӢгҒ®3еҖӢгҒҡгҒӨгҒ®зө„гҒ«гҒӨгҒ„гҒҰгӮӮпјҢеҗҢгҒҳгӮҲгҒҶгҒ«зңӢжқҝд»ҳгҒҚгҒ®гҒЁгҒҚгҒҜ
гҒ®зө„гҖҚгҒ®гӮҲгҒҶгҒӘпјҢгҒ»гҒӢгҒ®3еҖӢгҒҡгҒӨгҒ®зө„гҒ«гҒӨгҒ„гҒҰгӮӮпјҢеҗҢгҒҳгӮҲгҒҶгҒ«зңӢжқҝд»ҳгҒҚгҒ®гҒЁгҒҚгҒҜ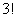 йҖҡгӮҠж•°гҒҲгҒҰгҒ„гӮӢгӮҸгҒ‘гҒӘгҒ®гҒ§пјҢд»®гҒ®зңӢжқҝгӮ’д»ҳгҒ‘гҒҹгҒЁгҒҚгҒ®еҲҶгҒ‘ж–№
йҖҡгӮҠж•°гҒҲгҒҰгҒ„гӮӢгӮҸгҒ‘гҒӘгҒ®гҒ§пјҢд»®гҒ®зңӢжқҝгӮ’д»ҳгҒ‘гҒҹгҒЁгҒҚгҒ®еҲҶгҒ‘ж–№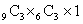 йҖҡгӮҠгӮ’пјҢ3!гҒ§гӮҸгҒЈгҒҰ(зңӢжқҝгҒҜгҒҡгҒ—гҒ—гҒҰ)
йҖҡгӮҠгӮ’пјҢ3!гҒ§гӮҸгҒЈгҒҰ(зңӢжқҝгҒҜгҒҡгҒ—гҒ—гҒҰ)
гҒЁгҒӘгӮӢгӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ
| (5)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’пјҢ1еҖӢпҪҘ4еҖӢпҪҘ4еҖӢгҒ®3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮ |
гҖҖд»ҠеәҰгӮӮгҒҫгҒҡд»®гҒ®зңӢжқҝA,B,CгӮ’гҒӨгҒ‘гҒҰзө„гҒҝеҲҶгҒ‘гҒҷгӮӢгҒ“гҒЁгӮ’иҖғгҒҲгӮҲгҒҶгҖӮ
пјҲйҖҡгӮҠпјү
гҖҖд»ҠеәҰгҒ®е ҙеҗҲ(4)гҒЁйҒ•гҒҶгҒЁгҒ“гӮҚгҒҜпјҢдёӯиә«гҒҢ1еҖӢгҒ гҒ‘гҒ®зө„гҒ«гҒӨгҒ„гҒҰгҒҜпјҢзңӢжқҝгӮ’гҒҜгҒҡгҒ—гҒҰгӮӮд»–гҒ®4еҖӢгҒ®зө„гҒЁгҒҜеҖӢж•°гҒ®йҒ•гҒ„гҒӢгӮүеҢәеҲҘгҒҢгҒӨгҒҸгҒЁгҒ„гҒҶгҒ“гҒЁгҒ§гҒӮгӮӢгҖӮ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | гҖҖ | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | гҖҖ | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Aзө„ |  |
 |
вҖҰ |  |
 |
вҖҰ |  |
 |
| Bзө„ |     |
    |
вҖҰ |     |
    |
вҖҰ |     |
    |
| Cзө„ |     |
    |
вҖҰ |     |
    |
вҖҰ |     |
    |
гҖҖдёҠгҒ®иЎЁгҒ§A,B,CгҒ®зңӢжқҝгӮ’еӨ–гҒ—гҒҹе ҙеҗҲпјҢеҲҶгҒ‘ж–№1пҪҘ2гҒҜеҗҢгҒҳеҲҶгҒ‘ж–№гҒ«гҒӘгӮҠпјҢеҲҶгҒ‘ж–№3пҪҘ4гӮӮеҗҢгҒҳеҲҶгҒ‘ж–№гҒ«гҒӘгӮҠпјҢеҲҶгҒ‘ж–№5пҪҘ6гӮӮеҗҢгҒҳеҲҶгҒ‘ж–№гҒ«гҒӘгӮӢгҖӮзңӢжқҝгӮ’еӨ–гҒ—гҒҹе ҙеҗҲгҒ«еҢәеҲҘгҒҢгҒӘгҒҸгҒӘгҒЈгҒҰгҒ—гҒҫгҒҶгҒ®гҒҜBзө„гҒЁCзө„гҒ®2зө„гҒ гҒ‘гҒӘгҒ®гҒ§пјҢдҪҷиЁҲгҒ«ж•°гҒҲгҒҰгҒ„гҒҹгҒ®гҒҜпјҢзңӢжқҝBгҒЁCгҒ®д»ҳгҒ‘ж–№гҒ®ж–№жі•гҒ®еҲҶгҒ гҒ‘гҒЁгҒ„гҒҶгҒ“гҒЁгҒ«гҒӘгӮӢгҖӮгҒқгҒ®зңӢжқҝгҒ®д»ҳгҒ‘ж–№гҒҜBпҪҘCгҒ®2ж–Үеӯ—гҒ®дёҰгҒ№ж–№гҒ®еҲҶгҒ гҒ‘гҒӘгҒ®гҒ§ 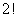 йҖҡгӮҠгҒ§гҒӮгӮӢгҖӮгҒӨгҒҫгӮҠпјҢ
йҖҡгӮҠгҒ§гҒӮгӮӢгҖӮгҒӨгҒҫгӮҠпјҢ
| зө„гҒ®еҢәеҲҘгҒҢгҒӮгӮӢгҒЁгҒҚгҒ®2!йҖҡгӮҠгҖҖвҶ’гҖҖзө„гҒ®еҢәеҲҘгҒҢгҒӘгҒ„гҒЁгҒҚгҒ®1йҖҡгӮҠ |
гҒЁгҒ„гҒҶй–ўдҝӮгҒ§гҒӮгӮӢгҖӮгҒқгҒ“гҒ§д»®гҒ®зңӢжқҝгӮ’д»ҳгҒ‘гҒҹгҒЁгҒҚгҒ®еҲҶгҒ‘ж–№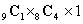 йҖҡгӮҠгӮ’пјҢ2!гҒ§гӮҸгҒЈгҒҰ(зңӢжқҝгҒҜгҒҡгҒ—гҒ—гҒҰ)
йҖҡгӮҠгӮ’пјҢ2!гҒ§гӮҸгҒЈгҒҰ(зңӢжқҝгҒҜгҒҡгҒ—гҒ—гҒҰ)
гҒЁгҒӘгӮӢгӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ
| (6)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгӮҲгҒ„гҖӮ |
гҖҖ(3)гҒЁгҒ®йҒ•гҒ„гҒҜпјҢдёҖдәәеҪ“гҒҹгӮҠгҒ®еҸ–гӮҠеҲҶгҒҢжұәгҒҫгҒЈгҒҰгҒ„гҒӘгҒ„гҒ“гҒЁгҒ§гҒӮгӮӢгҖӮзҺүгҒ®гӮҶгҒҸгҒҲгӮ’1гҒӨгҒҡгҒӨиҝҪгҒЈгҒҰгҒ„гҒЈгҒҰгҒҝгӮҲгҒҶгҖӮ
вҖҰвҖҰ A,B,CгҒ®3йҖҡгӮҠгҒ®иЎҢгҒҚе ҙжүҖгҒҢгҒӮгӮӢгҖӮ
вҖҰвҖҰ еҗҢгҒҳгҒҸA,B,CгҒ®3йҖҡгӮҠгҒ®иЎҢгҒҚе ҙжүҖгҒҢгҒӮгӮӢгҖӮ
вҖҰвҖҰ еҗҢгҒҳгҒҸA,B,CгҒ®3йҖҡгӮҠгҒ®иЎҢгҒҚе ҙжүҖгҒҢгҒӮгӮӢгҖӮ
вҖҰвҖҰ еҗҢгҒҳгҒҸA,B,CгҒ®3йҖҡгӮҠгҒ®иЎҢгҒҚе ҙжүҖгҒҢгҒӮгӮӢгҖӮ
вҖҰвҖҰд»ҘдёӢеҗҢж§ҳ
гҒЁгҒ„гҒҶгӮҸгҒ‘гҒ§пјҢгҒ©гҒ®зҺүгӮӮ3йҖҡгӮҠгҒ®иЎҢгҒҚе ҙгҒҢгҒӮгӮӢгҖӮгҒқгҒ—гҒҰдёҖдәәеҪ“гҒҹгӮҠгҒ®еҸ–гӮҠеҲҶгҒҢжұәгҒҫгҒЈгҒҰгҒ„гҒӘгҒ„гҒ®гҒ§пјҢгҒҹгҒЁгҒҲе…ЁгҒҰгҒ®зҺүгҒҢAгҒ«иЎҢгҒЈгҒҰгҒ—гҒҫгҒЈгҒҰгӮӮж§ӢгӮҸгҒӘгҒ„гӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ(3)гҒ§гҒҜиЁұгҒ•гӮҢгҒӘгҒӢгҒЈгҒҹгҒ“гҒЁгҒ§гҒӮгӮӢгҖӮ
гҖҖгҒҷгӮӢгҒЁгҒ“гҒ®иЁҲз®—ж–№жі•гҒҜж„ҸеӨ–гҒ«еҚҳзҙ”гҒ§пјҢ3йҖҡгӮҠгҒ®иЎҢгҒҚйҒ“гӮ’жҢҒгҒЈгҒҹз•°гҒӘгӮӢзҺүгҒҢ9еҖӢгҒӮгӮӢгҒ®гҒ§пјҢ
гҒЁгҒӘгӮӢгҒ гҒ‘гҒ§гҒӮгӮӢгҖӮ
| (7)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҜгҒ„гҒӘгҒ„гӮӮгҒ®гҒЁгҒҷгӮӢгҖӮ |
гҖҖ(6)гҒҜз°ЎеҚҳгҒ§гӮӮпјҢ(7)гҒ®гӮҲгҒҶгҒ«пҪўеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒӘгҒ„пҪЈгҒЁгҒ—гҒҹе ҙеҗҲзӘҒеҰӮгҒЁгҒ—гҒҰйӣЈгҒ—гҒҸгҒӘгӮӢгҒ®гҒ§гҒӮгӮӢгҖӮеӨҡгҒҸгҒ®дәәгҒҢ(9)гҒӢгӮүгҒ®йҖЈжғігҒ§пҪўгҒЁгӮҠгҒӮгҒҲгҒҡ пҪҘ
пҪҘ пҪҘ
пҪҘ гӮ’3дәәгҒ«еҲҶгҒ‘гҒҰгҒҠгҒ‘гҒ°пјҢгҒӮгҒЁгҒҜиІ°гӮҸгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгҒ„гҒ„гҒӢгӮүвҖҰвҖҰпҪЈгҒЁиҖғгҒҲгҒҰеӨұж•—гҒҷгӮӢгҖӮгҒ“гҒ®иҖғгҒҲж–№гҒ гҒЁпјҢ
гӮ’3дәәгҒ«еҲҶгҒ‘гҒҰгҒҠгҒ‘гҒ°пјҢгҒӮгҒЁгҒҜиІ°гӮҸгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгҒ„гҒ„гҒӢгӮүвҖҰвҖҰпҪЈгҒЁиҖғгҒҲгҒҰеӨұж•—гҒҷгӮӢгҖӮгҒ“гҒ®иҖғгҒҲж–№гҒ гҒЁпјҢ пҪҘ
пҪҘ пҪҘ
пҪҘ гҒ®3еҖӢгҒҢеҝ…гҒҡйҒ•гҒҶдәәгҒ«иЎҢгҒҸгҒ“гҒЁгҒ«гҒӘгҒЈгҒҰгҒ—гҒҫгҒҶгҒҢпјҢе®ҹйҡӣгҒ«гҒҜ
гҒ®3еҖӢгҒҢеҝ…гҒҡйҒ•гҒҶдәәгҒ«иЎҢгҒҸгҒ“гҒЁгҒ«гҒӘгҒЈгҒҰгҒ—гҒҫгҒҶгҒҢпјҢе®ҹйҡӣгҒ«гҒҜ

 гҒҢе…ЁйғЁAгҒ•гӮ“гҒ«иЎҢгҒЈгҒҰгӮӮпјҢд»–гҒ®зҺүгҒ®гҒҶгҒЎжңҖдҪҺдёҖеҖӢгҒҡгҒӨгҒҢBгҒ•гӮ“гҒЁCгҒ•гӮ“гҒ«иЎҢгҒ‘гҒ°е•ҸйЎҢгҒӘгҒ„гӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ
гҒҢе…ЁйғЁAгҒ•гӮ“гҒ«иЎҢгҒЈгҒҰгӮӮпјҢд»–гҒ®зҺүгҒ®гҒҶгҒЎжңҖдҪҺдёҖеҖӢгҒҡгҒӨгҒҢBгҒ•гӮ“гҒЁCгҒ•гӮ“гҒ«иЎҢгҒ‘гҒ°е•ҸйЎҢгҒӘгҒ„гӮҸгҒ‘гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒ§пјҢд»•ж–№гҒҢгҒӘгҒ„гҒ®гҒ§дҪҷдәӢиұЎгҒ§иЎҢгҒҸгҒ“гҒЁгҒ«гҒҷгӮӢгҖӮеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гӮӢе ҙеҗҲгҒЁгҒ„гҒҶгҒ®гҒҜпјҢ2дәәгҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„(е…ЁйғЁгҒ®зҺүгҒҢ1дәәгҒ«иЎҢгҒҸ)е ҙеҗҲгҒЁпјҢ1дәәгҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„(2дәәгҒ§еұұеҲҶгҒ‘зҠ¶ж…Ӣ)гҒ®2йҖҡгӮҠгҒҢгҒӮгӮӢгҖӮгҒ“гӮҢгӮүгҒ®еҲҶгҒ‘ж–№гҒ®ж•°гӮ’(6)гҒ®зӯ”гҒӢгӮүгҒІгҒ„гҒҰгӮ„гӮӢгҒ®гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒҫгҒҡ2дәәгҒҢеҸ—гҒ‘еҸ–гӮүгҒҡпјҢе…ЁйғЁгҒ®зҺүгҒҢ1дәәгҒ«иЎҢгҒҸе ҙеҗҲгҒҜпјҢAгҒ«е…ЁйғЁиЎҢгҒҸе ҙеҗҲгҒЁBгҒ«е…ЁйғЁиЎҢгҒҸе ҙеҗҲгҒЁCгҒ«е…ЁйғЁиЎҢгҒҸе ҙеҗҲгҒ®3йҖҡгӮҠгҒ гҒ‘гҒ§гҒӮгӮӢгҖӮ
гҖҖеҺ„д»ӢгҒӘгҒ®гҒҜ1дәәгҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҒ§гҒӮгӮӢгҖӮдҫӢгҒҲгҒ°AгҒҢеҸ—гҒ‘еҸ–гӮҢгҒҡпјҢе…ЁгҒҰгҒ®зҺүгӮ’BгҒЁCгҒ®2дәәгҒ§еҲҶгҒ‘еҗҲгҒҶеҲҶгҒ‘ж–№гҒҜпјҢз•°гҒӘгӮӢ9еҖӢгҒ®зҺүгӮ’2дәәгҒ«еҲҶгҒ‘гӮӢгҒ“гҒЁгӮ’иҖғгҒҲгҒҰпјҢ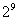 йҖҡгӮҠгҒЁгҒӘгӮҠгҒқгҒҶгҒӘгӮӮгҒ®гҒ гҖӮгҒЁгҒ“гӮҚгҒҢгҒ“гҒ®
йҖҡгӮҠгҒЁгҒӘгӮҠгҒқгҒҶгҒӘгӮӮгҒ®гҒ гҖӮгҒЁгҒ“гӮҚгҒҢгҒ“гҒ®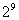 йҖҡгӮҠгҒ®дёӯгҒ«гҒҜпјҢе…ЁйғЁгҒҢBгҒ«иЎҢгҒҸе ҙеҗҲгҒЁе…ЁйғЁгҒҢCгҒ«иЎҢгҒҸе ҙеҗҲгҒҫгҒ§еҗ«гҒҫгӮҢгҒҰгҒ„гӮӢгҒ®гҒ§гҒӮгӮӢгҖӮгҒ“гӮҢгӮүгҒҜе®ҹйҡӣгҒ«гҒҜ1дәәеҚ гӮҒгҒЁгҒӘгӮӢгҒ®гҒ§пјҢд»ҠиЁҲз®—гҒ—гӮҲгҒҶгҒЁгҒ—гҒҰгҒ„гӮӢгҖҢ1дәәгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҖҚгҒ«еҪ“гҒҰгҒҜгҒҫгӮүгҒӘгҒ„гҖӮгҒқгҒ“гҒ§AгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„еҲҶгҒ‘ж–№гҒ®з·Ҹж•°гҒҜпјҢ
йҖҡгӮҠгҒ®дёӯгҒ«гҒҜпјҢе…ЁйғЁгҒҢBгҒ«иЎҢгҒҸе ҙеҗҲгҒЁе…ЁйғЁгҒҢCгҒ«иЎҢгҒҸе ҙеҗҲгҒҫгҒ§еҗ«гҒҫгӮҢгҒҰгҒ„гӮӢгҒ®гҒ§гҒӮгӮӢгҖӮгҒ“гӮҢгӮүгҒҜе®ҹйҡӣгҒ«гҒҜ1дәәеҚ гӮҒгҒЁгҒӘгӮӢгҒ®гҒ§пјҢд»ҠиЁҲз®—гҒ—гӮҲгҒҶгҒЁгҒ—гҒҰгҒ„гӮӢгҖҢ1дәәгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҖҚгҒ«еҪ“гҒҰгҒҜгҒҫгӮүгҒӘгҒ„гҖӮгҒқгҒ“гҒ§AгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„еҲҶгҒ‘ж–№гҒ®з·Ҹж•°гҒҜпјҢ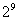 гҒӢгӮү
гҒӢгӮү 2гӮ’гҒІгҒ„гҒҰпјҢ
2гӮ’гҒІгҒ„гҒҰпјҢ
йҖҡгӮҠ
гҒЁгҒӘгӮӢгҖӮгҒқгҒ—гҒҰеҗҢгҒҳгҒ“гҒЁгҒҢBгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҒЁCгҒ гҒ‘гҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҒ«гҒӨгҒ„гҒҰгӮӮгҒ„гҒҲгӮӢгҒ®гҒ§пјҢзөҗеұҖиӘ°гҒӢ1дәәгҒҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„е ҙеҗҲгҒ®з·Ҹж•°гҒҜ
йҖҡгӮҠ
гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒ“гӮҢгӮүгҒ®дҪҝгҒЈгҒҰпјҢиӘ°гӮӮгҒҢжңҖдҪҺ1еҖӢгҒҜеҸ—гҒ‘еҸ–гӮӢгӮҲгҒҶгҒӘеҲҶгҒ‘ж–№гӮ’иЁҲз®—гҒҷгӮӢгҖӮгҒқгӮҢгҒ«гҒҜ
е…ЁгҒҰгҒ®еҲҶгҒ‘ж–№ вҲ’ е…ЁйғЁгҒҢ1дәәгҒ«иЎҢгҒҸеҲҶгҒ‘ж–№вҲ’ 2дәәгҒ гҒ‘гҒ§еҲҶгҒ‘еҗҲгҒҶеҲҶгҒ‘ж–№
гҒЁиЁҲз®—гҒҷгӮҢгҒ°иүҜгҒ„гҒ®гҒ§
39-3-(29-2)Г—3 = 39-3гғ»29+3 = 18150 йҖҡгӮҠ
гҒЁгҒӘгӮӢгҖӮ
| (8)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгӮҲгҒ„гҖӮ (9)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’3дәәгҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—еҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҜгҒ„гҒӘгҒ„гӮӮгҒ®гҒЁгҒҷгӮӢгҖӮ |
гҖҖгҒ“гҒ®2е•ҸгҒ«гҒӨгҒ„гҒҰгҒ®иӘ¬жҳҺгҒҜпјҢпҪўйҮҚиӨҮзө„гҒҝеҗҲгӮҸгҒӣпҪЈгӮ’еҸӮз…§гҒ—гҒҰгӮӮгӮүгҒ„гҒҹгҒ„гҖӮгҒқгӮҢгҒһгӮҢгҒ®зӯ”гҒҜпјҢж¬ЎгҒ®йҖҡгӮҠгҒ§гҒӮгӮӢгҖӮ
(8)
в—Ӣ(зҺү)вҖҰвҖҰ9еҖӢ
в– (д»•еҲҮгӮҠ)вҖҰвҖҰ2еҖӢгҖҖгҖҖиЁҲ11еҖӢгӮ’дёҰгҒ№гҒҰ
(9)гҖҖгҒҫгҒҡзҺү3еҖӢгӮ’дҪҝгҒЈгҒҰпјҢ3дәәгҒ«1еҖӢгҒҡгҒӨгӮ’жёЎгҒ—гҒҰгҒ—гҒҫгҒ„пјҢж®ӢгӮҠгҒ®6еҖӢгҒ«гҒӨгҒ„гҒҰпјҢеҸ—гҒ‘еҸ–гӮүгҒӘгҒ„дәәгҒҢгҒ„гҒҰгӮӮгӮҲгҒ„гҒЁгҒ—гҒҰ3дәәгҒ«еҲҶгҒ‘гӮӢгҒ“гҒЁгӮ’иҖғгҒҲгӮӢгҖӮ
в—Ӣ(зҺү)вҖҰвҖҰ6еҖӢ
в– (д»•еҲҮгӮҠ)вҖҰвҖҰ2еҖӢгҖҖгҖҖиЁҲ8еҖӢгӮ’дёҰгҒ№гҒҰ
| (10)гҖҖеҢәеҲҘгҒ®гҒӨгҒӢгҒӘгҒ„зҺү9еҖӢгӮ’3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—зө„гҒ«еҢәеҲҘгҒҜд»ҳгҒ‘гҒӘгҒ„гҖӮ |
гҖҖеҗ„зө„гҒ«A,B,CгҒЁгҒ„гҒҶзңӢжқҝгӮ’гҒӨгҒ‘гҒҰзҺүгӮ’еҲҶгҒ‘гҒҰгҒҠгҒ„гҒҰпјҢеҫҢгҒӢгӮүзңӢжқҝгӮ’гҒҜгҒҡгҒӣгҒ°гӮҲгҒ•гҒқгҒҶгҒӘгӮӮгҒ®гҒ гҒҢпјҢеҗ„зө„гҒ®еҖӢж•°гҒҢжұәгҒҫгҒЈгҒҰгҒ„гҒӘгҒ„гҒЁгҒҚгҒҜеҚұйҷәгҒӘгҒ®гҒ§гҒӮгӮӢгҖӮ(4)гҒЁ(5)гҒ§гӮ„гҒЈгҒҹгӮҲгҒҶгҒ«пјҢеҗҢгҒҳеҖӢж•°гҒҢе…ҘгҒЈгҒҹзө„гҒҢгҒ„гҒҸгҒӨгҒӮгӮӢгҒӢгҒ«гӮҲгҒЈгҒҰпјҢзңӢжқҝеӨ–гҒ—гҒ®гҒҹгӮҒгҒ«еҲҶжҜҚгҒ«жҢҒгҒЈгҒҰгҒҸгӮӢйҡҺд№—гҒҢеӨүгӮҸгӮӢгҒӢгӮүгҒ§гҒӮгӮӢгҖӮдҫӢгҒҲгҒ°2еҖӢпҪҘ3еҖӢпҪҘ4еҖӢгҒ«еҲҶгҒӢгӮҢгӮӢеҲҶгҒ‘ж–№гҒҜпјҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜж¬ЎгҒ®3!йҖҡгӮҠгҒ§гҒӮгӮҠпјҢ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Aзө„ | в—Ӣв—Ӣ | в—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ |
| Bзө„ | в—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣ |
| Cзө„ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣ |
гҒ“гҒ®е ҙеҗҲгҒҜ
| зңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜ3!йҖҡгӮҠгҖҖвҶ’гҖҖзңӢжқҝгҒҢгҒӘгҒ„е ҙеҗҲгҒҜ1йҖҡгӮҠ |
гҒЁгҒӘгӮӢгҒ®гҒ§пјҢ3!гҒ§гӮҸгӮүгҒӘгҒ‘гӮҢгҒ°гҒӘгӮүгҒӘгҒ„гҒҜгҒҡгҒ§гҒӮгӮӢгҖӮгҒЁгҒ“гӮҚгҒҢдҫӢгҒҲгҒ°1еҖӢпҪҘ4еҖӢпҪҘ4еҖӢгҒ«еҲҶгҒӢгӮҢгӮӢеҲҶгҒ‘ж–№гҒҜпјҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒ§гӮӮж¬ЎгҒ®3йҖҡгӮҠгҒ—гҒӢгҒӘгҒ„гҖӮ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 |
| Aзө„ | в—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ |
| Bзө„ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ |
| Cзө„ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣв—Ӣв—Ӣв—Ӣ | в—Ӣ |
гҖҖгҒ“гҒ®гӮҲгҒҶгҒ«пјҢ3зө„гҒ®зҺүгҒ®ж•°гҒҢе…ЁйғЁйҒ•гҒҶе ҙеҗҲгҒЁпјҢеҗҢгҒҳеҖӢж•°гҒ®зө„гҒҢгҒӮгӮӢе ҙеҗҲгҒ§пјҢзңӢжқҝгҒҢгҒӨгҒ„гҒҰгҒ„гӮӢгҒЁгҒҚгҒ®еҲҶгҒ‘ж–№гҒ®ж•°гҒҢйҒ•гҒҶгҒ®гҒ§пјҢзңӢжқҝгӮ’гҒӨгҒ‘гҒҰеҲҶгҒ‘гҒҹе ҙеҗҲгҒ®ж•°гӮ’гҒӮгҒЈгҒ•гӮҠ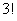 гҒ§гӮҸгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгҒӘгҒ„гҖӮгҒқгҒ“гҒ§гҒ“гҒ®гӮҲгҒҶгҒӘпҪўеҲҶгҒ‘гӮӢгӮӮгҒ®гҒ«еҢәеҲҘгҒӘгҒ—пјҢзө„гҒ«еҢәеҲҘгҒӘгҒ—пјҢеҖӢж•°гӮӮжұәгҒҫгҒЈгҒҰгҒ„гҒӘгҒ„пҪЈе ҙеҗҲгҒҜпјҢж•°гҒҲдёҠгҒ’гҒ®йҒ“гҒ—гҒӢж®ӢгҒЈгҒҰгҒ„гҒӘгҒ„гҖӮеҖӢж•°гҒ®е°‘гҒӘгҒ„зө„гҒӢгӮүдёҰгҒ№гҒҰгҒ„гҒҸй Ҷз•ӘгҒ§пјҢж•°гҒҲдёҠгҒ’гӮҲгҒҶгҖӮ
гҒ§гӮҸгӮӢгҒ“гҒЁгҒҢгҒ§гҒҚгҒӘгҒ„гҖӮгҒқгҒ“гҒ§гҒ“гҒ®гӮҲгҒҶгҒӘпҪўеҲҶгҒ‘гӮӢгӮӮгҒ®гҒ«еҢәеҲҘгҒӘгҒ—пјҢзө„гҒ«еҢәеҲҘгҒӘгҒ—пјҢеҖӢж•°гӮӮжұәгҒҫгҒЈгҒҰгҒ„гҒӘгҒ„пҪЈе ҙеҗҲгҒҜпјҢж•°гҒҲдёҠгҒ’гҒ®йҒ“гҒ—гҒӢж®ӢгҒЈгҒҰгҒ„гҒӘгҒ„гҖӮеҖӢж•°гҒ®е°‘гҒӘгҒ„зө„гҒӢгӮүдёҰгҒ№гҒҰгҒ„гҒҸй Ҷз•ӘгҒ§пјҢж•°гҒҲдёҠгҒ’гӮҲгҒҶгҖӮ
гҖҢв—ӢгҖҚгҖҖгҖҢв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(1, 1, 7)
гҖҢв—ӢгҖҚгҖҖгҖҢв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(1, 2, 6)
гҖҢв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(1, 3, 5)
гҖҢв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(1, 4, 4)
гҖҢв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(2, 2, 5)
гҖҢв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—Ӣв—ӢгҖҚгҖҖ(2, 3, 4)
гҖҢв—Ӣв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—ӢгҖҚгҖҖгҖҢв—Ӣв—Ӣв—ӢгҖҚгҖҖ(3, 3, 3)
д»ҘдёҠгҒ®иЁҲ7йҖҡгӮҠгҒ§гҒӮгӮӢгҖӮ
гҖҖеҝөгҒ®гҒҹгӮҒд»ҳгҒ‘еҠ гҒҲгҒҰгҒҠгҒҸгҒҢпјҢгғҖгғ–гӮҠгӮ’йҒҝгҒ‘гӮӢгҒҹгӮҒгҒ«еҖӢж•°гҒ®е°‘гҒӘгҒ„й ҶгҒ«дёҰгҒ№гҒҰгҒ„гӮӢгҒ®гҒ§пјҢ(1, 4, 4)еҖӢгҒ®зө„гҒҝеҗҲгӮҸгҒӣгҒ®гҒӮгҒЁгҒҜпјҢ(1, 5, 3)гҒ§гҒҜгҒӘгҒҸ(2, 2, 5)гҒ§гҒӮгӮӢгҒ—((1, 5, 3) гҒ®зө„гҒҝеҗҲгӮҸгҒӣгҒҜ(1, 3, 5)еҖӢгҒ®зө„гҒҝеҗҲгӮҸгҒӣгҒЁеҗҢгҒҳгҒ§гҒӮгӮӢ)пјҢеҗҢгҒҳзҗҶз”ұгҒӢгӮү(2, 3, 4)гҒ®гҒӮгҒЁгҒҜ(2, 4, 3)гҒ§гҒҜгҒӘгҒҸ(3, 3, 3)гҒӘгҒ®гҒ§гҒӮгӮӢгҖӮ
| (11)гҖҖ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•гҒҜдҪ•йҖҡгӮҠгҒӮгӮӢгҒӢгҖӮгҒҹгҒ гҒ—зө„гҒ«еҢәеҲҘгҒҜгҒӨгҒ‘гҒҡпјҢ0еҖӢгҒ®зө„гҒҜгҒӮгҒЈгҒҰгҒҜгҒӘгӮүгҒӘгҒ„гҖӮ |
вҳ…д»ҘдёӢгҒҜе№іжҲҗ29е№ҙ11жңҲ19ж—ҘгҒ«иҝҪиЁҳгҒ—гҒҹи§Јжі•гҒ§гҒҷгҖӮ
гҖҖгҒ“гҒ®е ҙеҗҲгҒҜ(10)гҒЁгҒҜйҒ•гҒЈгҒҰпјҢгҖҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜn!йҖҡгӮҠгҖҖвҶ’гҖҖзңӢжқҝгҒҢгҒӘгҒ„е ҙеҗҲгҒҜ1йҖҡгӮҠгҖҚгӮ’иҖғгҒҲгӮҢгҒ°иүҜгҒ„гҖӮгҒӘгҒңгҒӘгӮүпјҢдҫӢгҒҲгҒ°2еҖӢгғ»3еҖӢгғ»4еҖӢгҒ«еҲҶгҒӢгӮҢгҒҰгҒ„гӮӢгҒЁгҒҚгҒҜгӮӮгҒЎгӮҚгӮ“гҖҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜ3!йҖҡгӮҠгҖҖвҶ’гҖҖзңӢжқҝгҒҢгҒӘгҒ„е ҙеҗҲгҒҜ1йҖҡгӮҠгҖҚгҒЁгҒӘгӮӢгҒҢпјҢ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Aзө„ |   |
  |
   |
   |
    |
    |
| Bзө„ |    |
    |
  |
    |
  |
   |
| Cзө„ |     |
   |
    |
  |
   |
  |
1еҖӢгғ»4еҖӢгғ»4еҖӢгҒ®гӮҲгҒҶгҒ«пјҢеҖӢж•°гҒҢеҗҢгҒҳгҒ§гҒӮгӮӢзө„гҒҢгҒӮгҒЈгҒҰгӮӮпјҢдёӯиә«гҒҢз•°гҒӘгӮӢгҒ®гҒ§гӮ„гҒҜгӮҠгҖҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜ3!йҖҡгӮҠгҖҖвҶ’гҖҖзңӢжқҝгҒҢгҒӘгҒ„е ҙеҗҲгҒҜ1йҖҡгӮҠгҖҚгҒЁгҒӘгӮӢгҖӮ
| гҖҖ | еҲҶгҒ‘ж–№1 | еҲҶгҒ‘ж–№2 | еҲҶгҒ‘ж–№3 | еҲҶгҒ‘ж–№4 | еҲҶгҒ‘ж–№5 | еҲҶгҒ‘ж–№6 |
| Aзө„ |  |
 |
    |
    |
    |
    |
| Bзө„ |     |
    |
 |
    |
 |
    |
| Cзө„ |     |
    |
    |
 |
    |
 |
гҖҖзөҗеұҖпјҢгҒ©гӮ“гҒӘеҖӢж•°гҒ®зө„еҲҶгҒ‘гҒ§гҒӮгҒЈгҒҰгӮӮпјҢгҖҢзңӢжқҝгҒҢгҒӮгӮӢе ҙеҗҲгҒҜn!йҖҡгӮҠгҖҖвҶ’гҖҖзңӢжқҝгҒҢгҒӘгҒ„е ҙеҗҲгҒҜ1йҖҡгӮҠгҖҚгҒЁгҒӘгӮӢ
гҖҖгҒқгҒ“гҒ§пјҢгҖҢ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’еҢәеҲҘгҒ®гҒӮгӮӢ3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•(0еҖӢгҒ®зө„гҒҜгҒӘгҒ„)гҖҚгӮ’ 3! гҒ§еүІгӮҢгҒ°иүҜгҒ„гҒ“гҒЁгҒ«гҒӘгӮӢгҒ®гҒ гҒҢпјҢгҖҢ9еҖӢгҒ®з•°гҒӘгӮӢзҺүгӮ’еҢәеҲҘгҒ®гҒӮгӮӢ3зө„гҒ«еҲҶгҒ‘гӮӢж–№жі•(0еҖӢгҒ®зө„гҒҜгҒӘгҒ„)гҖҚгҒҜ (7)гҒ§зӯ”гҒҲгҒҹгӮӮгҒ®гҒ§гҒӮгӮӢгҒӢгӮүпјҢгҒқгӮҢгӮ’еҲҶеӯҗгҒЁгҒ—гҒҰ 3! гҒ§еүІгӮҢгҒ°иүҜгҒ„гҒ“гҒЁгҒ«гҒӘгӮӢгҖӮеҫ“гҒЈгҒҰпјҢ
гҒЁгҒӘгӮӢгҖӮ
вҳ…д»ҘдёӢгҒҜе№іжҲҗ29е№ҙ11жңҲ19ж—Ҙд»ҘеүҚгҒӢгӮүжҺІијүгҒ—гҒҰгҒ„гҒҹи§Јжі•гҒ§гҒҷгҖӮ
гҖҖгҒ“гӮҢгҒҜгҒӢгҒӘгӮҠйӣЈгҒ—гҒ„гҖӮеҗ„зө„гҒ«д»®гҒ®зңӢжқҝгӮ’гҒӨгҒ‘гҒҰзҺүгӮ’еҲҶгҒ‘гҒҰгҒҠгҒ„гҒҰпјҢеҫҢгҒӢгӮүзңӢжқҝгӮ’гҒҜгҒҡгҒҷгҒ®гҒҢеҚұйҷәгҒӘгҒ®гҒҜ(10)гҒЁеҗҢгҒҳгҒ§гҒӮгӮӢгҖӮгҒӢгҒЁгҒ„гҒЈгҒҰж•°гҒҲдёҠгҒ’гӮҲгҒҶгҒЁгҒҷгӮӢгҒЁз•°гҒӘгӮӢзҺүгҒ§гҒӮгӮӢгҒ гҒ‘гҒ«еҲҶгҒ‘ж–№гҒҢгҒӮгҒҫгӮҠгҒ«еӨҡгҒҸгҒҰеӨ§еӨүгҒ§гҒӮгӮӢгҖӮд»•ж–№гҒҢгҒӘгҒ„гҒ®гҒ§гҒҫгҒҡеҗ„зө„гҒ®еҖӢж•°гӮ’жұәгӮҒгҒҰгҒӢгӮүпјҢеҗ„зө„гҒ«еҲҶгҒ‘гҒҰгҒ„гҒҸгҒЁгҒ„гҒҶж®өйҡҺгӮ’иёҸгӮ“гҒ§гҒ„гҒ“гҒҶгҖӮ
гҖҖеҗ„зө„гҒ®еҖӢж•°гҒ®жұәгӮҒж–№гҒҜ(10)гҒЁеҗҢгҒҳгҒ§гҒӮгӮӢгҖӮгҒқгҒ—гҒҰгҒқгӮҢгҒһгӮҢгҒ®еҖӢж•°гҒ®еҲҶгҒ‘ж–№гҒ«гҒӨгҒ„гҒҰпјҢзө„гҒҝеҗҲгӮҸгҒӣгҒ®ж•°гӮ’иҖғгҒҲгӮӢгҖӮеҖӢж•°гҒҢжұәгҒҫгҒЈгҒҰгҒ„гҒҰпјҢеҗ„зө„гҒ®еҢәеҲҘгҒҢгҒӘгҒ„е ҙеҗҲгҒ®еҲҶгҒ‘ж–№гӮ’иЁҲз®—гҒҷгӮӢгҒ®гҒ§гҒӮгӮӢгҖӮ
гҖҖгҒҫгҒҡпјҢеҗ„зө„гҒ®еҖӢж•°гҒҢ(1, 1, 7)гҒЁеҲҶгҒӢгӮҢгӮӢгҒӘгӮӢеҲҶгҒ‘ж–№гҒҜ
гҖҖ
ж¬ЎгҒ« (1, 2, 6)гҒЁгҒӘгӮӢеҲҶгҒ‘ж–№гҒҜ
(1, 3, 5)гҒЁгҒӘгӮӢеҲҶгҒ‘ж–№гҒҜ
(1, 4, 4)гҒҜ
(2, 2, 5)гҒҜ
(2, 3, 4)гҒҜ
(3, 3, 3)гҒҜ
д»ҘдёҠгӮ’е…ЁгҒҰгҒҹгҒ—гҒҰпјҢ
гҒЁгҒӘгҒЈгҒҹгҖӮ