令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
反復試行の確率の最大値
問題 1つのさいころを続けて35回投げたとき,6の目が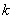 回出る確率を 回出る確率を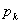 とする。(ただし とする。(ただし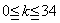 とする。) とする。)(1) (2) |
前節で反復試行の確率は説明したから,(1)をさっさとやってしまおう。6の目が出る回数が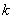 回,あるいは
回,あるいは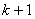 回というように文字で指定されているが,やることは前節と同じだから,気を確かに持って計算しよう。
回というように文字で指定されているが,やることは前節と同じだから,気を確かに持って計算しよう。
まず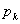 についてだが,35回中
についてだが,35回中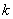 回6が出るということは,35回中
回6が出るということは,35回中 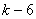 回は6以外が出るということだ。すると出かたの通り数は
回は6以外が出るということだ。すると出かたの通り数は
6 …… 枚
○(6以外をあらわす) …… 枚
計35枚
を並べる並べ方の数だけあるから
通りである。
そして,1通り当たりの確率は,
であるから,35回中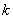 回6が出る確率すなわち
回6が出る確率すなわち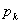 は,
は,
……①
である。また,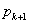 については,①の式の
については,①の式の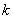 の代わりに
の代わりに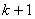 を代入すればいいので,
を代入すればいいので,
となる。これで(1)は終わった。
問題は(2)だ。もし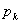 が単なる2次関数だったら平方完成すればいい。あるいは微分(←数Ⅱ・数Ⅲで習う)できる式だったら,微分して増減表を考えればいい。しかしこの式は微分は出来ないし,そもそも数Ⅰの問題なのだからもっと基礎的な考え方で解けなければおかしいというものだ。
が単なる2次関数だったら平方完成すればいい。あるいは微分(←数Ⅱ・数Ⅲで習う)できる式だったら,微分して増減表を考えればいい。しかしこの式は微分は出来ないし,そもそも数Ⅰの問題なのだからもっと基礎的な考え方で解けなければおかしいというものだ。
ではどうするかというと,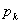 と
と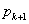 の大小比べをするのである。そして
の大小比べをするのである。そして
その結果をもとにして最大の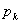 を探すことになる。
を探すことになる。
たとえば,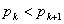 となるのは,
となるのは,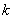 が何のときだろう? それを求めるために
が何のときだろう? それを求めるために
……*
に(1)の答を代入して計算をするのである。*の式に①と②を代入するとこうなる。
えらく大変に見えるかもしれないけれど,実際にはどんどん約分できるので大丈夫だ。
∴
……③
特に2行目から3行目の分母の払い方が重要で,各辺の分母を見比べてやると,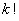 と
と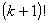 については,
については,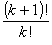 が
が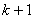 となることが,そして
となることが,そして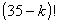 と
と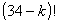 についても,
についても,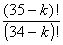 が
が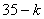 になることが即座にわかって貰いたい。
になることが即座にわかって貰いたい。
こうしてわかったことは,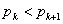 ……*となるのは
……*となるのは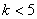 のとき,つまり
のとき,つまり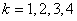 のときだということである(注:
のときだということである(注: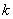 は回数を表わす数だから,当然整数である。しかも0以上だ)。 つまり
は回数を表わす数だから,当然整数である。しかも0以上だ)。 つまり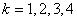 のときに*の式が成り立つということだから,実際に*に
のときに*の式が成り立つということだから,実際に*に 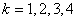 を代入すると,
を代入すると,
が成り立つことがわかる。つまり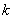 が4以下のときは,もう1回余計に出る確率のほうが大きいということである。これを点グラフにしてみると次のような感じになる。
が4以下のときは,もう1回余計に出る確率のほうが大きいということである。これを点グラフにしてみると次のような感じになる。
次に,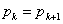 となるのは
となるのは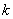 が何のときかを考える。もっとも考えるとはいっても,*の式の中の
が何のときかを考える。もっとも考えるとはいっても,*の式の中の 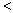 が
が 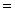 になっただけだから,その結果も③の式の
になっただけだから,その結果も③の式の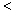 を
を 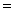 にするだけですむ。つまり
にするだけですむ。つまり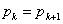 となるのは
となるのは 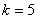 のときである。すると
のときである。すると
が成り立つことがわかるから,これを先の点グラフに書き加えると次のようになる。
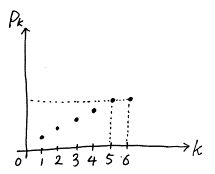
そして最後に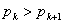 となるのは
となるのは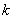 が何のときかを考えるが,これも*の式の不等号をひっくり返したものであるから,結果も③の式の不等号をひっくり返して,
が何のときかを考えるが,これも*の式の不等号をひっくり返したものであるから,結果も③の式の不等号をひっくり返して,
となる。つまり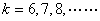 で成り立つというわけである。すなわち
で成り立つというわけである。すなわち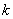 が6以上のときは,もう1か出でる確率のほうが低いということだから,これを更に点グラフに書き加えると次のようになる。
が6以上のときは,もう1か出でる確率のほうが低いということだから,これを更に点グラフに書き加えると次のようになる。
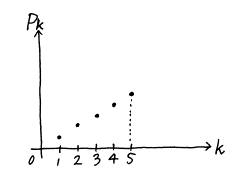
さて,この図を見れば,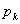 がもっとも大きくなるのは
がもっとも大きくなるのは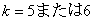 のときであることが良くわかる。このように反復試行の確率の最大値を考えるときには,
のときであることが良くわかる。このように反復試行の確率の最大値を考えるときには,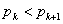 となるような0以上の整数
となるような0以上の整数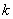 の範囲と,
の範囲と,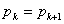 となるような整数
となるような整数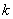 の値と,
の値と,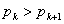 となるような整数
となるような整数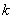 の範囲を求めて,それらをもとにして
の範囲を求めて,それらをもとにして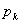 の点グラフをかくとわかりやすい。
の点グラフをかくとわかりやすい。
| 解答 |
(1) 35回中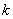 回6が出る確率は,
回6が出る確率は,
……①
である。また,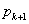 については,①の式の
については,①の式の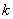 に
に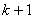 を代入して
を代入して
である。
(2) まず,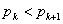 となるような
となるような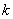 の範囲を求める。①・②より,
の範囲を求める。①・②より,
すなわち
のとき
となる。
同様にして,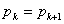 となる
となる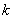 の値を求めると,
の値を求めると,
となる。
同様にして,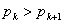 となるような
となるような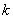 の範囲を求めると,
の範囲を求めると,
すなわち
のとき
となる。
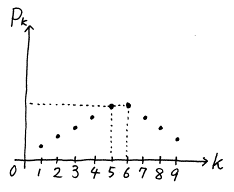
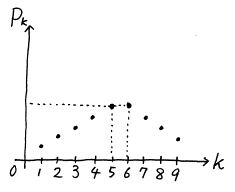
これらをまとめてグラフにすると,その概形は次のようになる。
よってグラフより,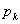 が最大となるのは
が最大となるのは 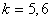 のときである。
のときである。
まとめ
|
| 練習問題 問題1 1の目が出る確率が4分の1であるさいころがある。このさいころを30回投げるとき, (1) 1の目が (2) 1の目が何回出る確率が最も大きいか。 |
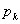 および
および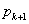 を求めよ。
を求めよ。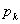 が最大となるのは,
が最大となるのは,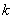 がいくらのときか。
がいくらのときか。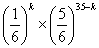
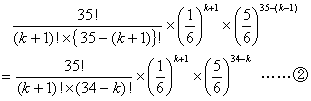
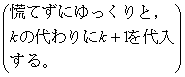
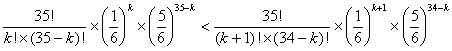

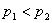
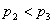
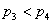
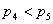
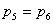
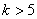
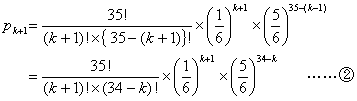
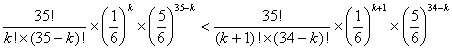
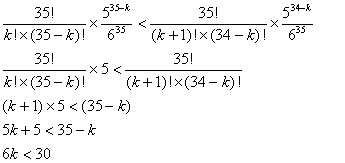
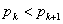 となるような0以上の整数
となるような0以上の整数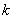 の範囲
の範囲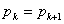 となるような0以上の整数
となるような0以上の整数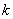 の値
の値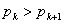 となるような0以上の整数
となるような0以上の整数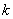 の範囲
の範囲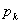 の点グラフをかいて考える。
の点グラフをかいて考える。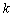 回出る確率
回出る確率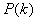 を求めよ。
を求めよ。