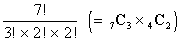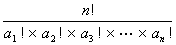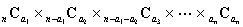令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
組み合わせのもう一つの考え方
| 問題
|
A, B, C, D, Eの5人から3人を選ぶ選び方について,通常習う
以外の方法を考えてみよう。
| A | B | C | D | E |
| ○ | ○ | ○ | × | × |
| ○ | ○ | × | ○ | × |
| ○ | ○ | × | × | ○ |
| ○ | × | ○ | ○ | × |
| ○ | × | ○ | × | ○ |
| ○ | × | × | ○ | ○ |
| × | ○ | ○ | ○ | × |
| × | ○ | ○ | × | ○ |
| × | ○ | × | ○ | ○ |
| × | × | ○ | ○ | ○ |
ところが,この表の見方を変えてみると,
の計5個の並べ方を全部表したものになっているともいえるだろう。
つまり,5人から3人選ばれる(2人漏れる)選び方 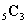 は,○(当選券に相当する)を3個と,×(落選券に相当する)を2個を5人の前に並べる並べ方の数だけあると考えられるわけだ。そしてその並べ方は
は,○(当選券に相当する)を3個と,×(落選券に相当する)を2個を5人の前に並べる並べ方の数だけあると考えられるわけだ。そしてその並べ方は
と計算できるから,
だ。
この考え方を一般化すると, n個の異なるものからr個選ぶ選び方 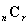 は
は
の計n個の並べ方の数だけあることになるので,
|
と書きかえられるわけである。
この考え方は組分けでも有効で,例えばA〜Gの7人を,い組(3人組),ろ組(2人組),は組(2人組)の3組に分けるなら,
| A | B | C | D | E | F | G |
| い | い | い | ろ | ろ | は | は |
| い | い | い | ろ | は | ろ | は |
| い | い | い | ろ | は | は | ろ |
| い | い | い | は | ろ | ろ | は |
| い | い | い | は | ろ | は | ろ |
| い | い | い | は | は | ろ | ろ |
| い | い | ろ | い | ろ | は | は |
| い | い | ろ | い | は | ろ | は |
| い | い | ろ | い | は | は | ろ |
 |
 |
 |
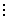 |
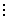 |
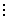 |
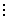 |
の計7枚のカードの並べ方の数だけ分け方があると考えられるから,
と計算できるわけだ。
一般には,n個の異なるものを,異なる組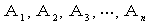 (各々
(各々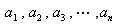 個からなる組で,
個からなる組で,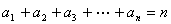 とする)に分ける方法は,
とする)に分ける方法は,
と計算できる。これはもちろん,
としても同じことだが,文字定数を含む計算の場合は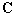 を使わない上の式の方がすっきりした式になるというものだ。
を使わない上の式の方がすっきりした式になるというものだ。
| 解答 |
異なるn個のものからr個取る組み合わせを決めるために,その異なるn個のものの前に
○……r枚
×……
枚 計n枚
を並べることを考えると,その並べ方は
である。ゆえに 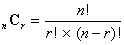 である。
である。
| 練習問題 [難] 1から10までの番号をつけた10枚の札から4枚抜き取るとき,抜き取った4枚のうち少なくとも2枚の番号が連続する抜き取り方は何通りあるか。 (東京医大・改題) |
解説
「少なくとも2枚の番号が連続する抜き取り方」を直接考えるのは難しいので,
[全ての抜き取り方]−[番号が隣り合わない抜き取り方]
と考える(余事象というヤツだ)。
まず,異なる10枚の札から4枚を抜き取る方法は,10C4=210通り。
次に,異なる10枚から番号が隣り合わないように4枚抜き取る方法だが,次のように考えればよい。○を4枚と×を6枚用意して,それらを○が隣り合わないように全部並べる並べ方を考える。まず×を全部並べておいて
××××××
その両端と隙間(計7箇所)から4箇所選んで,○を入れる入れ方の数だけ並べ方があるから,7C4=35通り。
よって,抜き取った4枚のうち少なくとも2枚の番号が連続する抜き取り方は
210−35=175通り。
(市販の問題集に載っている解答は,私が見る限りとんでもなくめんどう臭い解答ばかりだったのだけど,何でかな?)
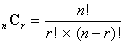 を説明せよ
を説明せよ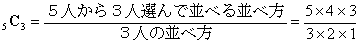
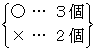

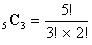

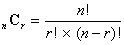 (この式は暗記ではなく理解しておくこと)
(この式は暗記ではなく理解しておくこと)