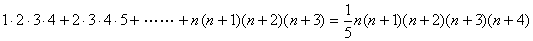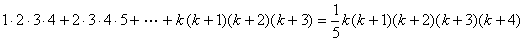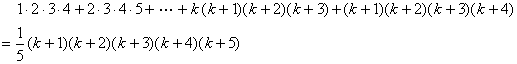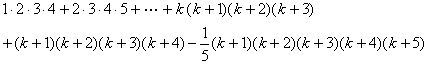令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
数学的帰納法とは?
| 問題 nを自然数とするとき,次の式が成り立つことを証明せよ。 |
Σで計算しようとすると,nの4乗がでてくるので困ったことに計算ができません。確かに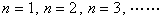 などと代入してみると成り立つのはわかりますが,証明する相手は1, 2, … ではなく,nです。全てのnについて成り立つことを示さないといけないのです。nは無限に続くので,ひとつひとつ代入していってもきりがありません。「
などと代入してみると成り立つのはわかりますが,証明する相手は1, 2, … ではなく,nです。全てのnについて成り立つことを示さないといけないのです。nは無限に続くので,ひとつひとつ代入していってもきりがありません。「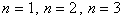 で成り立ったのだから,全部成り立つでしょう」というのは認められません。「じゃあ,成り立つことが永遠に続くという証拠は?」と突かれてそれまでです。
で成り立ったのだから,全部成り立つでしょう」というのは認められません。「じゃあ,成り立つことが永遠に続くという証拠は?」と突かれてそれまでです。
そこで考え出されたのが,数学的帰納法の骨格の
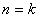 で成り立つなら, で成り立つなら,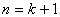 でも成り立つ でも成り立つ |
という,魔法の鍵なのです。このことさえ示せれば,後はこの鍵が自動的に,「n = 2で成り立つなら,n = 3でも成り立つし,n = 3でも成り立つならn = 4でも…」と,無限に続くnの全てについて,次々と示してくれることになるわけです。
ただしこの鍵は,最初に成り立つnがあってこそ使えるものですから,この鍵を実際に使うには,最初の一歩の使い出し点を用意してやらねばいけません。それが数学的帰納法のもう1つのポイントである,
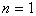 のとき成り立つ のとき成り立つ |
ことを示すことなのです。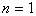 のときに成り立つことが示せれば,魔法の鍵はこれを出発点として無限に働くわけです。
のときに成り立つことが示せれば,魔法の鍵はこれを出発点として無限に働くわけです。
さて,先の等式を実際に証明してみましょう。
まず,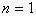 のときですが,左辺は
のときですが,左辺は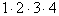 だけになりますし,右辺は
だけになりますし,右辺は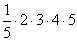 となって,いずれも24で等しいことがわかります。
となって,いずれも24で等しいことがわかります。
次に肝腎の
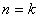 で成り立つなら, で成り立つなら,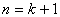 でも成り立つ でも成り立つ |
ことの証明ですが,具体的に n = k のときの式と,n = k +1 のときの式を書いてみるとわかりやすくなります。
まず のときは
のときは
……(1)
次に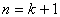 のときの式は,
のときの式は,
……(2)
となります。魔法の鍵の証明は,
| (1)が成り立つならば(2)も成り立つ |
ことを証明する,つまり(1)を使って(2)を証明すればいいわけです。(2)を証明するには,「(2)の左辺−(2)の右辺=0」が示せればよいですから,(2)の左辺−(2)の右辺を計算しはじめると,
(2)の左辺−(2)の右辺
=
……★
となりますが,このうち1行目の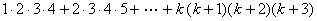 は,(1)より
は,(1)より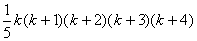 と等しいので,★の式にこれを代入してみると,
と等しいので,★の式にこれを代入してみると,
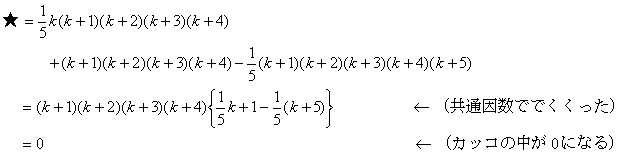
となり,めでたく証明できたことになります。
実際に数学的帰納法を使うときにはこのように,n=k のときの式((1)の式)と,n=k+1 のときの式((2)の式)をきちんと書いてみて,(1)を使って(2)を証明すればいい,と考えれば俄然証明しやすくなります。