令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
個数の処理と確率の計算における，場合の数の数え方の違い
あるくじ引きで，１本の大当たりくじと２本の小当たりくじ，そして７本のはずれくじがあるとしよう。このくじ引きを１本ひいて当たる確率を，
 |
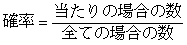を信じて次のように計算してもいいだろうか？
| 全ての場合の数 … 大当たり・小当たり・はずれの３通り。 当たりの場合の数… 大当たり・小当たりの２通り。 よって |
…（×） もちろんこれは間違いで，本当の答は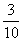 
である。大当たり，小当たりを合わせて当たりは３本，それに対してはずれは７本だからである。しかしくじを１本ひいたときの出かたは確かに３通りであるし，当たりは確かに２通りである。本数の違いで説明したいかも知れない。しかし「個数の処理」の計算では，確かに同じものは区別しないで計算したはずではないか。このギャップをどうやって説明しようか？
そこで確率の神様に登場してもらう。人間には同じものに見えるはずの小当たり２本も，はずれくじ７本も，確率の神様ならなんでもお見通しで，ちゃんと区別していて別々に数えているはずだ。今，大当たりを◎で，小当たりを○で，はずれを×で表すと，
| 人間が見ると… ◎○○×××××××と見えて，○同士，×同士の区別がつかない 神様が見ると… ◎○1○2×1 ×2 ×3×4×5×6 ×7と見えて，全てを区別している |
というわけである。
すると確率の神様による場合の数の計算では，○1と○2は添え数字がついているから別物であり，×1〜×7も同様に別物だと考えて，
| 全ての場合の数 … ◎ ○1 ○2×1×2×3 ×4×5×6×7 の10通り。 当たりの場合の数… ◎○1○2 の３通り。 よって |
…（○）と，正しく計算されるわけである。
このような単純な確率ならば，誰でも無意識に正答できるが，玉の種類が多くなったときなどには，
|
個数の処理→ 同じに見えるものは同じもの。
確率の計算→ 同じに見えるものでも，個体が違えば別のもの。添え数字をふって考える。 |
という原則に注意をしてもらいたい。
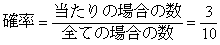