常用対数とはどんな数か？

　このページでは，「そもそも対数って何？」という方のために，前半ではまず「対数とはどんな数か？」をベースに対数の基本を説明し，それに加えて常用対数の特長をお伝えします。

10³ = 1000

　これは，「10を3乗すると1000である」という意味です。これを見方を変えると，「10を1000にする指数は，3である」と言うこともできます。このときの「3」を，「10を1000にする指数」という意味を込めて，

3 = log₁₀1000

　と書くことにしたのです。つまり log₁₀1000 は元々「10を1000にする指数」という意味であり，これを「1000の常用対数は，3である」ということにしたのです。これが，常用対数の基本です。一般には

y = 10^x

　であるとき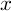，「は，10 を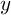にする指数」という意味で，

x = log₁₀ y

と書き，その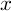を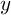，の常用対数と呼ぶわけです。念のため繰り返しますが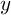，の常用対数が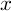であるということは，10 の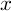乗が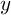である，ということです。（ちなみにこの式の"10"の部分を「底」と呼びます。常用対数は底が10である対数のことですが，常用対数以外の対数では，底は1以外の正の数ならなんでもありえます。また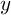を「真数」と呼びます。）

　さて，常用対数の便利さを理解するために必要な，重要な法則を一つ確認しておきます。指数法則の a^maⁿ = a^m+n というものです。これは例えば，10²✕10³ を考えると，10を2回かけたものと10を3回かけたものをかけ合わせるのだから，結局10をかける回数は合計5回，つまり 10²✕10³ = 10✕10✕10✕10✕10 = 10²⁺³ となることを想像すれば，さほど難しくはないと思いますが如何でしょうか。ポイントは，10のナントカ乗同士をかけ算する場合，その指数部分はかけ算になるのではなくて，足し算になるという点です。

　ここで，「345は10の何乗か？」を考えてみます。10を2乗すれば100ですし，10を3乗すれば1000ですから，10を345にする指数，つまり345の常用対数があるとすれば，それは2と3の間にあるはずです。そこで，345を無理やり 100✕3.45 と分解して考えてやります。なぜ分解するかというと，1から10の間の小数についておおよそ10の何乗であるのか，つまり常用対数がおおよそ何であるのかが，常用対数表というマニアック（？）な表に書いてあるからです。そうすると，100は10の2乗ですし，3.45はその常用対数表を参考にするとおおよそ10の0.5378乗，つまり log₁₀3.45 = 0.5378 であることがわかります。そうすると，100✕3.45 つまり 345は，10の2乗かけるおおよそ10の0.5378乗であり，先ほどの指数法則によれば，おおよそ10の「2+0.5378乗」つまり10の2.5378乗だということになります。つまり log₁₀345 = 2.5378 （345の常用対数はおおよそ 2.5378) であったわけです。

345 = 100 ✕ 3.45
≒ 10² ✕ 10^0.5378
= 10^2.5378

　こうして見ると，常用対数の整数部分（この場合は2.5378の，2の部分）は，元の数の「桁数-1」を表すことになります。常用対数の一つの特長に，整数部分を見ると桁数がわかる，ということがあります（元の数の桁数が，常用対数の整数部分+1となるわけです。）。

　今度は，345✕234を，常用対数的な方法で考えてみます。先ほどの345のときと同じように，234が10の何乗であるかを調べると，234 = 100✕2.34ですが，100は10の2乗であり，常用対数表によれば 2.34はおおよそ 0.3692とわかります。従って 234はおおよそ10の 2.3692ということになります。そうすると，345✕234は，おおよそ，10の2.5378乗かける 10の2.3692乗ということになるわけですが，指数法則によって，このナントカ乗の部分を足すことができることになります。

345 ✕ 234 ≒ 10^2.5378 ✕ 10^2.3692
= 10^{(2.5378+2.3692)}
= 10^4.9070

となりました。そうすると今度は 10の4.9070乗を，10の4乗かける10の0.9070乗と考えなおして，今度は常用対数表の中から 0.9070に近い値を探すと，0.9069というのが8.07の常用対数であることがわかるので，

10^4.9070 = 10^(4+0.9070)
                = 10⁴ ✕ 10^0.9070
                ≒ 10000 ✕ 8.07
                = 80700

と，おおよその値がわかりました。実際には 345✕234 は 80730ですから，厳密な計算ではありませんが，自然科学で「有効数字」を考え合わせる場合には，理由は省略しますがこれで十分ということになります。このように，元々かけ算であったものを，常用対数を考えることによって，足し算で済ませることができるというのが常用対数のまたひとつの特長であるわけです。ちなみに今の計算で，常用対数が4.9070となった時点で，この数字の桁数は 4+1= 5 であることがわかります。

平成25年5月5日記す

対数とはどんな数か？を参照する | 対数の基本公式と，底の変換公式を参照する