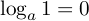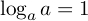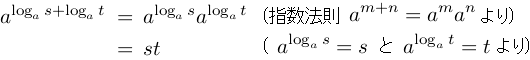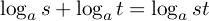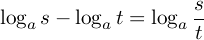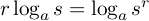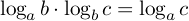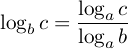令和4年3月11日: 東日本大震災トリアージ訴訟を掲載
対数の基本公式と,底の変換公式
log はその基本からして,これまでに使ってきた記号に比べて複雑ですから,その計算方法も一筋縄では行きません.(対数の基本は,こちらで確認してください.)
まずはその中でも簡単なものから説明しましょう.
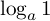 は,「
は,「 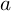 を1にする指数」ですから,
を1にする指数」ですから,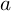 がどんな数であっても 0 ですし(
がどんな数であっても 0 ですし( 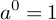 ),
),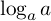 は「
は「 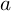 を
を 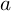 にする指数」ですから,当然
1 です.(
にする指数」ですから,当然
1 です.( 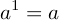 )
)
次に 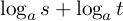 が,どう計算できるかを考えます.そのためには,
が,どう計算できるかを考えます.そのためには,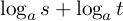 が,結局は「
が,結局は「 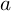 を何にする指数」なのかを,実際に
を何にする指数」なのかを,実際に 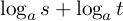 を
を 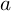 の指数とした
の指数とした 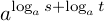 を計算することによって調べることにします.計算すれば,
を計算することによって調べることにします.計算すれば,
となります.すなわち,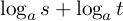 は,「
は,「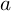 を
を 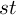 にする指数」とわかりました.ということは,
にする指数」とわかりました.ということは,
であったわけです.
次は 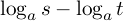 ですが,
ですが,
と計算できますから,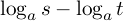 は「
は「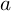 を
を
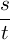 にする指数」とわかりました.つまり
にする指数」とわかりました.つまり
なのです.
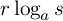 はどうでしょうか.これも
はどうでしょうか.これも 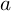 の指数にした
の指数にした 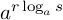 を計算してみるのですが,指数の順序を変えて計算すれば,
を計算してみるのですが,指数の順序を変えて計算すれば,
←(
です。)
です.「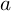 を
を 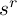 にする指数」ですから,
にする指数」ですから,
と変形できます.
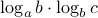 はどうでしょう.
はどうでしょう.
←(
)
ということで,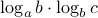 は,
は,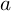 を
を 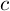 にする指数だとわかります.(まず一つめの指数
にする指数だとわかります.(まず一つめの指数 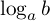 が,
が,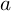 を
を 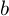 にして,次に二つめの指数
にして,次に二つめの指数 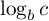 が,
が,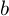 を
を 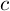 にしたわけです.)
にしたわけです.)
この公式は,この形では教科書には出てきませんが,二つの対数のかけ算で,片方の真数がもう片方の底と同じなときに,一つの対数に直せるので,この形で理解しておくと便利です.普通の教科書などには,この両辺を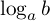 でわってある形,すなわち
でわってある形,すなわち
だけが載っています.これを底の変換公式といい,底を無理矢理変えるために使います.左辺から右辺に変えるときに新たに登場する底の値は,なんでもよいのです.(ただし正でしかも 1 以外です.)